Hello

Le dessin ci dessous t'aide t il?

je n'avais pas pensé a considérer la surface de l'eau comme ne lentille de rayon de courbure infini

Merci beaucoup

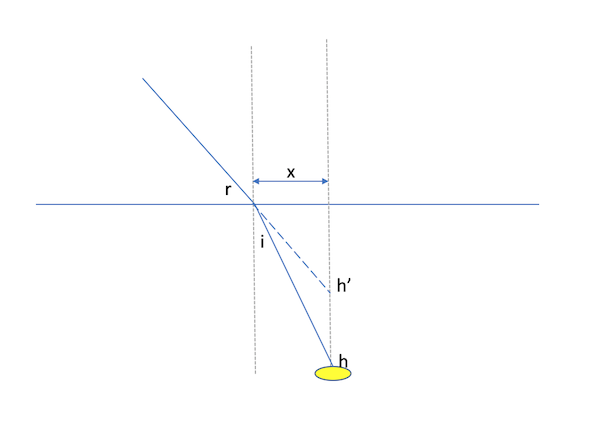
Zut, j'avais pas mis la légende à mon schéma que je croyais explicite

La ligne d'eau (la surface de la piscine) c'est la droite horizontale!
c'est à dire un dioptre (un dioptre est une surface séparant deux milieux transparents homogènes et isotropes, d'indices de réfraction différents)

(une lentille = 2 dioptres)

Tu appliques la loi de Descartes / réfraction pour mettre en relation les angles i et r

Puis tu fais un peu de géométrie pour exprimer x en fonction de h puis de h'

Et à l'occasion tu fais tendre x vers 0 (si le besoin s'en fait sentir) puisque l'on regarde l'eau sous un angle proche de la normale (à la surface)

Ca va mieux?

bonsoir ce qui me chiffone c'est que dans votre schéma on ne regarde pas la piece avec un angle d'incidence proche de la normale :/

pas grave!  Tu le fais pour x quelconque puis tu fais tendre x vers 0 ce qui correspond bien à l'observateur arrive à la verticale de la pièce

(c'est ce que je crois avoir déjà écrit, mais de me répéter, point ne m'ennuie )

parfait ahah un grand merci et d'excellentes fetes de fin d'années

itou

N'hésite pas à rapporter ici le résultat de ton raisonnement et des tes calculs (cela s'appelle la capitalisation du savoir   )