Bonjour Morgane55,

il va falloir quand même que tu apprennes à faire des dessins plus lisibles... tu as le choix entre les dessiner directement sur un ordi (OpenOffice, Géogébra ou autre), ou plus simplement sur une feuille de papier que tu scannes ; tu peux aussi la photographier et en faire un fichier gif que tu joins à ton message (voir ici [lien], question Q5). Les axes se tracent avec une règle, les cercles avec un compas !

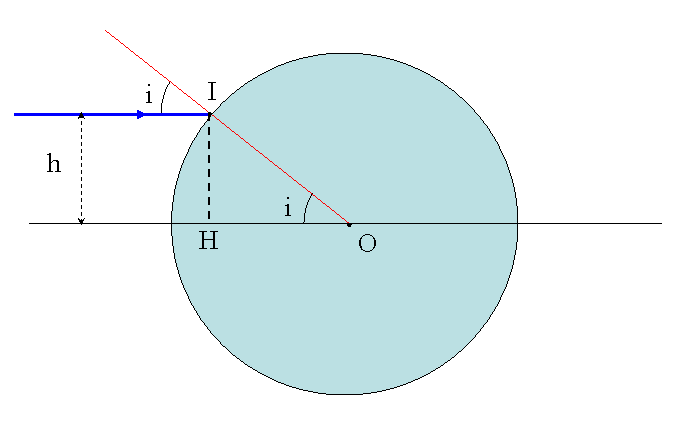
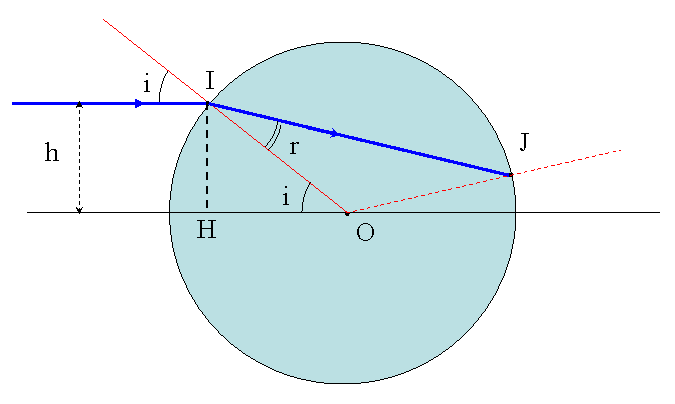
Regarde la figure ci-dessous, que j'ai légèrement modifiée : l'angle d'incidence i du rayon bleu se retrouve comme l'un des angles du triangle OHI. Comme c'est un triangle rectangle en H, avec HI = h et OI = R, on a tout de suite sini = h/R = x. OK ?

A toi de continuer, tu devrais faire facilement la question 2. Et quant à ta réponse 3, rappelle-toi une chose : tu ne peux pas comparer h, qui est une longueur mesurée en m, avec n, qui est un indice de réfraction et qui donc n'a pas d'unité.

A toi.

Merci beaucoup pour la question on a donc sin i = h/R = x donc i = arcsin h/R = arcsin x.

2. Le rayon de refraction = rayon incident non ?

i = arcsinx est une bonne réponse, mais inutile ici puisque la loi de Descartes fait intervenir directement sini.

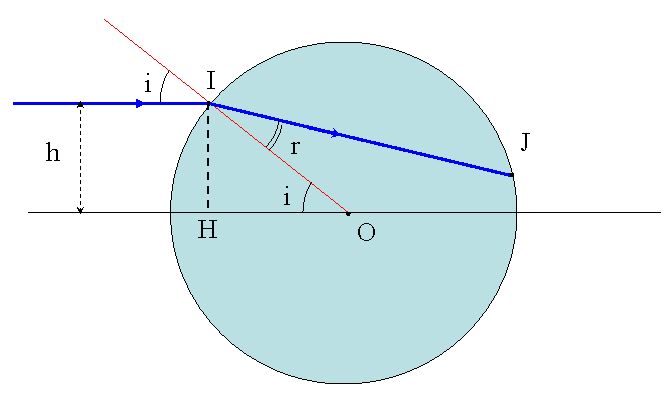
"Le rayon de refraction = rayon incident non ?"  Houlà... tu oublies justement la réfraction en I, qui s'écrit n₁.sini = n₂.sinr, r étant l'angle entre le rayon lumineux réfracté (donc qui se propage dans la boule) et la normale au point d'impact (droite rouge sur mon schéma). En posant n₁ = 1 (air) et n₂ = n (gaz contenu dans la boule), cette loi s'écrit sini = n.sinr, soit sinr = x/n.

A toi de tracer le rayon réfracté qui se déplace dans la boule (pour une valeur quelconque de x et de n), et de le prolonger jusqu'au point J où il va rencontrer de nouveau l'enveloppe de la boule. Que va-t-il lui arriver après ?

Il sera tracé entre la normale et le demi cercle en bas il me semble

Eh bien trace-le donc, comme il est demandé à la question 2. On verra ensuite si on peut passer à la question 3.

donc en rouge c'est r

Bravo pour le tracé de la figure, par rapport aux tracés à main levée précédents, ça s'arrange. En revanche, du point de vue de l'optique géométrique... c'est consternant. D'après ton schéma, le rayon réfracté en I s'en va directement vers O, et là il change brusquement de direction (on se demande bien pourquoi) pour sortir  finalement de la boule selon ton rayon rouge... !!
Tu ne tiens aucun compte des explications données par gbm dans un exercice analogue (celui-ci : ), et tu donnes nettement l'impression de ne rien comprendre à ce que tu fais.

Commence par relire ton cours de cette année, celui de seconde aussi si tu l'as encore (car les lois de Descartes sont étudiées en seconde dans le thème 3 - l'univers - chapitre 19 - l'observation des étoiles).
Voici ci-dessous la figure que j'attendais, et qui n'était pas difficile à obtenir. Essaie maintenant de terminer le tracé du rayon, après le point J.

Merci.. enfaite je comprends pas comment vous avez fait pour tracer votre rayon en bleu. Desolé si je suis bête j'ai lu mon cours mais je ne sais pas comment tracer à chaque fois.

Bonjour Morgane55,

ce n'est pas parce qu'on à des difficultés à comprendre qu'on est forcément bête : je n'ai jamais employé ce mot-là devant mes étudiants, et ne le ferai jamais ici. Cela dit, c'est vrai que mon précédent message était agressif, mais je l'ai fait volontairement : tu es si j'en crois ton profil en première année dans une fac (si tu me dis laquelle ça m'intéresserait), et le S₁, qui est un semestre pluridisciplinaire, contient entre autres de la physique... même si cela ne plaît pas à tous. En général la partie de la physique qui est retenue est justement l'optique géométrique, parce que c'est la plus simple et qu'elle fait appel à des acquis vus dès le lycée (notion de mesure algébrique en math, lois de Descartes en physique). Reconnais quand même que pour appliquer la loi de Descartes sur la réfraction, il suffit de calculer deux sinus, ce qui n'est pas insurmontable. Donc, si tu veux valider ton S₁, il est temps de s'y mettre. C'est ce signal d'alarme que j'ai voulu te donner.

Tu peux trouver les bases de l'optique géométrique ici : ; ne perds pas l'adresse de ce site, car il y a des fiches de cours sur toute les branches de la physique étudiées de la seconde à la terminale. Eventuellement, si tu m'écris sur mon adresse courriel (disponible en cliquant sur le personnage à côté de mon pseudo), je connaitrai la tienne et pourrai t'envoyer directement des explications, animations, diaporamas et autres) sur l'optique.

Pour l'instant, on va finir ici cet exercice :
Pour construire le rayon réfracté dans la boule, c'est très simple : le milieu incident est l'air (donc n₁ = 1) et le milieu enfermé dans la boule est un gaz (n₂ = n > 1). La loi sur la réfraction dit que lorsqu'on passe d'un milieu mins réfringent vers un milieu plus réfringent, l'angle de réfraction diminue car le rayon réfracté se rapproche de la normale. A retenir absolument ! C'est pourquoi j'ai représenté l'angle de réfraction r plus petit que l'angle d'incidence i. Pour calculer r, il faut connaître i et n : la loi de Descartes donne alors sini = n.sinr, soit sinr = sini/n = x/n ici puisqu'on a posé sini = x.
Exemple : avec x = 1/2 (soit i = 30°) et n = 4/3 (c'est beaucoup pour un gaz, mais peut importe c'est juste pour faire une application numérique), alors on trouve facilement r = 22°. Voilà pour le rayon qui se propage dans la boule.

Maintenant, regarde la figure ci-dessous, identique à la précédente mais avec le tracé de OJ en pointillé rouge. La deuxième réfraction va se produire en J, et OJ est la normale en J à la surface de la boule. Le nouvel angle d'incidence en J est donc (IJ, OJ). A ton avis, que vaut cet angle ? Si tu trouves la réponse, tu obtiendra facilement la nouvelle direction prise par le rayon qui va sortir en J.

A toi.

Daccord merci je suis en l1 maths-info et je voudrais faire une l2 maths-g après. Si j'ai bien compris alors la rayon refracte sera > que le rayon incident cette fois ci ? Donc il faut que je trouve l'angle J là. Le triangle IOJ est rectangle donc je dirais que l'angle IJ JO c'est le même que IJ IO

On y est presque... mis à part que le triangle IOJ est isocèle et non rectangle, et qu'on ne dit pas qu'un rayon est plus grand qu'un autre rayon (un rayon lumineux n'est pas une grandeur mesurable), on progresse...
Donc, si l'angle (IJ,OJ) vaut r, tu devrais tracer facilement le rayon qui va sortir de la boule en J.

Ca va faire un trait comme au début jon2 ? Car on inverse cette fois ci

Pardon je voulais dire non ? Et pas jon2

"Ca va faire un trait comme au début jon2 ? Car on inverse cette fois ci" : quelle pauvreté de langage !! "un trait", c'est un rayon lumineux... "au début" : au début de quoi ?  "on inverse" : c'est peut-être le morceau de phrase le plus juste car il évoque le principe du retour inverse de la lumière, mais je crois que tu ne l'as pas fait exprès...
Ma réaction est la même que celle exprimée sans mon post du 29-10-15 à 22:40 : fais le trracé et poste-le sur le forum. Tu peux capter mon dernier schéma en faisant une copie d'écran et en en faisant une image, en jpg ou en gif par exemple. Un logiciel de traitement d'image (photofiltre par exemple, très efficace et complètement gratuit) fera ça très bien, et te permettra de rajouter le tracé du rayon sur cette image.

D'accord merci je vous envoie la photo mercredi apres midi car là je n'ai pas d'ordinateur.

voilà

Impossible : quels sont les indices de réfraction dans la boule et en dehors ? Apprends ton cours et va voir le lien que je t'ai donné le 31-10-15 à 14:32.

Pour l'air c'est 1 et le gaz je sais pas mais il est plus grand l'indice

Exact. ALors, que fait un rayon lumineux qui passe d'un milieu d'indice n vers un milieu d'indice 1 ??

Le rayon lumineux il va continuer sa route non ? On prolonge le rayon en bleu

Apprends ton cours.

Mais ya rien dans mon cours c'est que des schémas

Je n'y crois pas, mais si c'est vrai va voir ici : chapitre 4, pages 44 et suivantes. C'est super bien expliqué.

Ii2 c'est bien l'angle  J ?

L'angle i₂ de quelle figure ? Donne-moi le numéro de page.

PS : "l'angle J" s'appelle en réalité IJO.

Bon cette fois je dirais que il y a réflexion totale

Je dis ca parce que on passe d'un milieu plus refringent à un milieu moins refringent

J'ai peut etre dit n'importe quoi mais je sais pas comment faire si non

moi aussi j'ai le même exercice dans un devoir et je sais pas comment faire franchement ça m'a beaucoup aidé les réponses en haut mais la suite je suis perdu ....

Tu es en quelle classe

Ce n'est pas une réflexion totale. Alors, si on résume :
-  Le rayon ne sort pas comme le rayon jaune de ton post du 04-11-15 à 13:08 ;
-  il ne continue pas en ligne droite, comme dans ton post du 04-11-15 à 15:13 ;
-  il ne subit pas de réflexion totale en J.

Alors, qu'est-ce qui reste ?

La réponse se trouve dans le cours que je t'ai demandé de consulter (mon post du 04-11-15 à 17:37), page 45 en bas.

NB : ce cours est un cours de niveau seconde...

bein moi je suis en 1 ere année licence et pour les autres questions Monsieur Prbebo??

ce que je pense d'apres le derniere commentaire le rayon vas en haut genre l'inverse de ce qui dans le post de 04/11 13.08 (le jaune)

Il mon te le rayon lumineux je dirais

Impossible, car le rayon réfracté doit toujours se trouver de l'autre côté de la normale (voir les schémas de vos cours,plus ceux des pages 44 et 45 du lien donné ci-dessus).

Alors, qu'est-ce qui reste ?

Bonsoir, je pense que le rayon de sortie sera confondu avec la droite OJ

Impossible, car cela voudrait dire que l'angle entre le rayon émergent et la normale OJ à la surface de la boule est nul. Revoyez une fois de plus les schémas du cours dont je vous ai donné le lien.

Et faites un effort pour proposer une réponse plausible, au lieu de répondre au hasard.

Vers le bas ?

Oui, mais complète ta réponse en traçant ce rayon sur le schéma que tu as posté le 04-11-15 à 13:08 (et en supprimant le rayon jaune).

Pour tracer ce rayon, tu peux remarquer que le rayon incident pénètre dans la boule au point I en faisant un angle  i  avec la normale au dioptre en ce point et s'y propage suivant un rayon réfracté faisant un angle  r  avec ladite normale.
Puis le rayon réfracté atteint le point J où il fait un angle  r  avec la normale en ce point.
Il émerge ensuite de la boule; quel angle fait-il alors avec la normale ? (réponse sans calcul)

Bonsoir Priam,

c'est en effet la réponse que j'attends depuis mon post du 30-10-15 à 19:16 (une semaine donc). On est dans un profil post-bac, cursus math-info au premier semestre suivi de math-g au second. Cet exercice ne devrait donc pas poser de difficulté pour morgane55, c'est pourquoi j'ai attendu patiemment que la réponse arrive de lui plutôt que de moi-même. Je laisse volontiers terminer cet exercice avec lui. Sans doute seras-tu plus efficace que moi.

L'angle R c'est l'angle i du debut

Je crois que tu as compris.
Plus en détail :
Le rayon incident au point J, formant un angle  r  avec la normale au dioptre, ressort dans l'air suivant un rayon réfracté qui fait avec la normale un angle égal à l'angle d'incidence  i  du rayon initial.
Il y a là une illustration du principe de retour inverse de la lumière : dans la région du point I, la direction du rayon lumineux est définie par l'angle  i , puis par l'angle  r . Si on inversait le sens de la lumière, celle suivrait le même trajet, qui serait alors défini par les mêmes angles  r , puis i . C'est ce dernier cas qu'on observe dans la région du point J.
Tu peux maintenant tracer exactement le rayon sortant au point J.

Je peux tracer la parallèle à  OI qui passe par J ?

Non. Le rayon qui sort du point J doit faire, avec la normale OJ, un angle égal à l'angle  i .

Oui je sais

Je cherche comment faire je sais que c'est simple

Il vaut 45○

As-tu tracé le rayon sortant, issu du point J ?