Inscription / Connexion Nouveau Sujet
optique
Bonsoir , svp pouvez vous m'aider a resoudre cet exercice et merci d'avance!
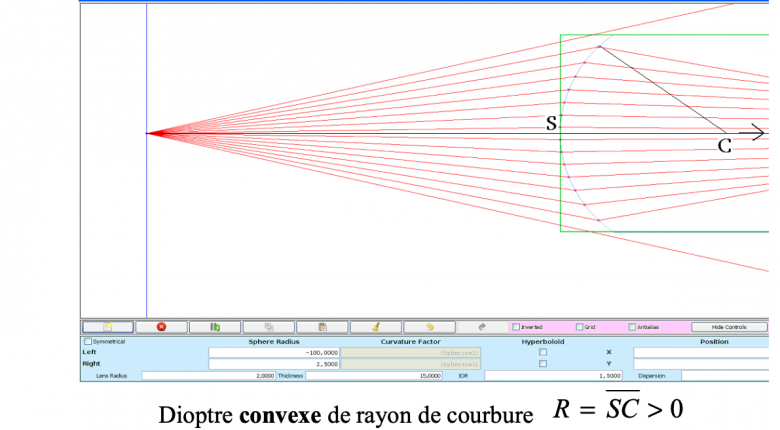
Donner SA' , position de l'image a travers un dioptre spherique convexe, d'un objet reel placé à 8cm du sommet S de ce dioptre.
On donne :sc rayon de courvure du dioptre =3cm , n1=1 et n2=1,33.
(Dans ma formule est-ce que je dois utiliser SA=8 ou -8 cm?)
Bonjour
Tu pourrais commencer par faire un schéma propre de la situation que tu pourrais poster ici. Ensuite revois ton cours sur les formules de conjugaison du dioptre plan. Tu peux poster tes réponses et poser des questions précises sur ce que tu ne comprends pas.
Ma question est la suivante :est-ce que je dois utiliser SA=8 ou -8 cm?
Parce que vu que ma lentille est convergente , l'image devrait etre normalement à droite ,
cependant lorsque j'utilise ma formule de conjugaison avec SA=-8cm(car normalement reel) , je trouve SA'<0
Si tu choisi comme sens positif le sens de propagation de la lumière en lui faisant correspondre sur ton schéma le sens gauche  droite, l'objet réel est donc à gauche du dioptre donc :
droite, l'objet réel est donc à gauche du dioptre donc :
Comme déjà écrit : je te conseille un schéma clair avec les tracés de quelques rayons particuliers, histoire de vérifier le réalisme des résultats obtenus par calculs. Les signes des mesures algébriques ne posent pas de problèmes avec un bon schéma.
Mon dessin devrait normalement ressembler à peu pres à celui là .
La relation de conjugaison:
[/tex]
Donc SA'<0  :(
:(
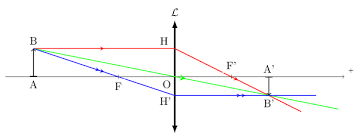
Tu traite le problème d'une lentille mince convergente. Or l'énoncé parle simplement d'un dioptre sphérique. Revois ton cours sur le sujet et refais ta figure.
Tu traite le problème d'une lentille mince convergente. Or l'énoncé parle simplement d'un dioptre sphérique. Revois ton cours sur le sujet et refais ta figure.
Je sais que c'est pas une lentille , mais j'ai deja dit que ce shema ressemblerait a peu pres au mien avec comme difference un dioptre spherique convergent!
ce shema ressemblerait a peu pres au mien
Je ne suis pas sûr qu'un correcteur, un jour d'examen ou de concours, se contenterait ainsi d'à peu près ...
Plus de renseignements et des schémas ici :
Si je comprends bien SC=3cm ?
Tu obtiens SA' <0 ; c'est effectivement la situation. Cela signifie que l'image est virtuelle. Le schéma que tu as fourni ne correspond donc pas "à peu près" à la réalité : il est complètement faux !
Tu obtiens SA' <0 ; c'est effectivement la situation. Cela signifie que l'image est virtuelle. [/u]
Mon dioptre est convergent donc l'image ne devrait pas normalement etre reelle?
Si non ? pourquoi? c'est tout ce que je demande à savoir!
Le fait d'obtenir SA'<0 suffit pour conclure que l'image est virtuelle. Pour bien comprendre pourquoi il en est ainsi, il faudrait faire un schéma en y plaçant un certain nombre de rayons particuliers, comme cela est fait sur le document que je t'ai fourni...
"ce shema ressemblerait a peu pres au mien" ; "l'image ne devrait pas normalement etre reelle? "
Je ne suis pas ton professeur mais tout de même : si tu veux vraiment progresser, tu vas devoir faire preuve d'un peu plus de rigueur...
Je pense que celui-là est le bon! (C'est vrai qu'il ne ressemble a rien en celui traité avec la lentille.) Sauf que je vois que l'image est toujours réelle , et dans votre document tous les cas avec des images virtuelles sont des cas où le dioptre est divergent.
P.S: j'apprecie vraiment votre aide ,e t merci pour le temps que vous me consacriez.
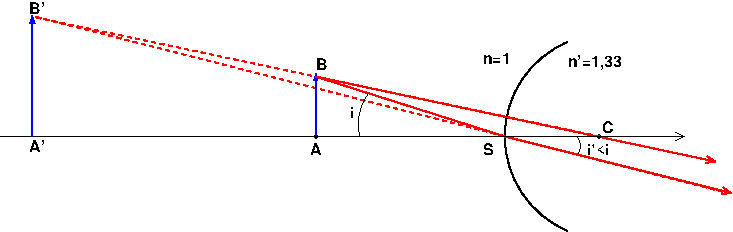
Non ! Il faut imaginer un objet réel AB à gauche du dioptre et tracer quelques rayons particuliers issus de B :
* le rayon passant par C n'est pas dévié ;
* le rayon passant par S vérifie la loi de Descartes avec l'axe optique comme normale au dioptre : n.sin(i)=n'.sin(i') ; comme n'>n : i'<i. Le rayon réfracté ne coupe pas le rayon précédent : il n'y a pas d'image réelle. En revanche, les prolongement de ces deux rayons se coupent en B' à gauche du dioptre. L'image de AB est donc virtuelle.
J'aurais pu commencer par positionner les foyer F et F' du dioptre et utiliser les propriétés de ces points...
Bien sûr : la figure n'est pas à l'échelle.
Je comprends mieux maintenant!
Mais est-ce que je dois toujours prendre l'objet comme segment AB (comme vous avez fait?) au lieu de prendre juste un point qui est sur l'axe optique comme j'ai fait précédemment??(Comment savoir dans quel cas je suis?)
Revois bien ton cours : les systèmes optiques centrés, c'est à dire admettant l'axe optique comme axe de symétrie, sont, dans les conditions d'utilisation de Gauss, des systèmes aplanétiques : ils donnent d'un objet plan perpendiculaire à l'axe optique, une image plane perpendiculaire à l'axe optique. En pratique, on détermine graphiquement l'image B' d'un point B puis on considère que A' est le projeté orthogonal de B' sur l'axe optique. Tu aurais pu t'intéresser à quelques rayons issus de A : l'étude est possible (voir document fourni précédemment) mais un peu plus compliquée.