Bonjour
La définition du diamètre angulaire que tu connais s'applique au cas de la question 1 ; plus généralement, elle s'applique lorsque ce que tu observes n'est pas situé à l'infini.
Dans le second cas, l'œil voit à travers la lentille l'image de AB rejetée à l'infini. La position de l'œil peut donc être quelconque derrière la lentille mais le placer en F' présente de l'intérêt dans certaines situations non étudiées ici semble-t-il. Le point A sur l'axe optique émet un faisceau de rayons qui ressortent de la lentille tous parallèles entre eux et parallèles à l'axe optique. Le point B émet un faisceau de rayons qui ressortent tous de la lentilles parallèles entre eux mais inclinés d'un angle ' par rapport à ceux issus de A. Cet angle ', mesuré en radian, est appelé diamètre angulaire ou diamètre apparent...

Merci pour votre réponse.

Je commence à comprendre un peu plus, mais par contre je ne comprends toujours pas pourquoi le corrigé donne AB/f'.

Comment, à partir de la définition citée dans mon premier message, peut-on savoir que tan '=AB/f' ?

Je suis vraiment désolé, je ne vois vraiment pas...

Merci encore pour l'aide.

Peux-tu scanner ton schéma concernant la question 2 et le poster  ? As-tu bien compris la définition de ' ?

Bien sûr, je vous envoie le schéma d'ici une dizaine de minutes.

A propos de la définition de alpha', j'ai l'impression de l'avoir comprise, mais en réalité je ne suis pas sûr de bien l'avoir comprise...

Une autre question aussi : je lis dans un livre : Lorsque l'on considère l'objet à l'infini : OA' (en algébrique) = f'.

Déjà, pourquoi dit-on cela ? Ensuite, est-ce vrai pour une lentille convergente ET pour une lentille divergente ?

Merci encore.

Pour n'importe quel système optique centré (admettant un axe optique), l'image A' d'un point objet A situé à l'infini sur l'axe optique est le point de l'axe optique appelé foyer image et noté très souvent F'. Le point image A' est donc confondu avec le foyer image F' dans ce cas particulier. De même, si A est confondu avec le foyer objet F, l'image est sur l'axe optique mais rejeté à l'infini : les rayons issus de A=F ressortent du dispositif optique parallèles à l'axe optique.

Voici les figures du corrigé.

Merci beaucoup pour vos explications.

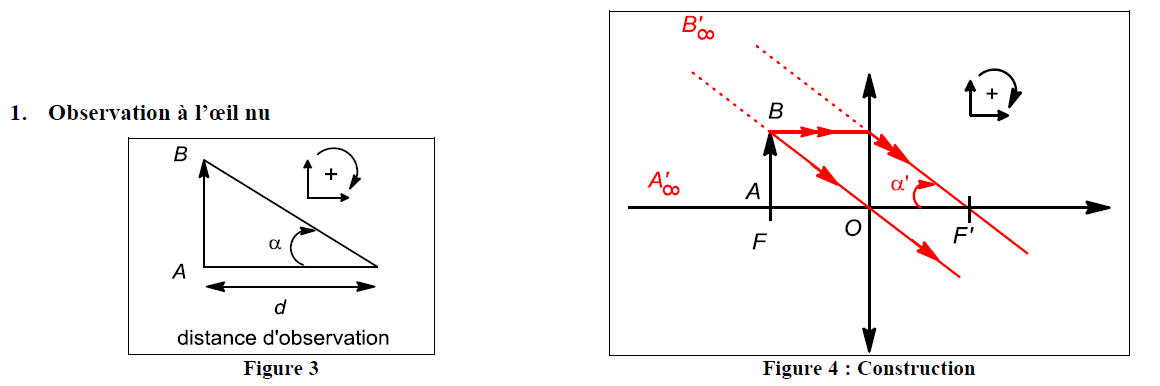
J'ajoute une dernière question : pourquoi sur la figure de droite ci-dessous il faut mettre des pointillés pour l'image à l'infini A'B' ? Pourquoi l'image n'est-elle pas à droite de la double-flèche symbolisant la lentille ?

Merci beaucoup pour votre message de 16h11, c'est plus clair pour l'infini, par contre, pas pour la définition de alpha et de alpha'...

Relis mes messages précédents.
Puisque A est confondu avec F, tous les rayons issus de A ressortent de la lentilles parallèlement à l'axe optique. Le rayon AO appartient à ce faisceau et n'est pas dévié. Ce résultat est considéré comme "évident" et ce tracé n'est pas fait pour ne pas alourdir la figure.
Tous les rayons issus de B ressortent de la lentille parallèlement entre eux. Deux de ces rayons sont tracés en rouge. On voit bien que l'angle entre les deux faisceaux est l'angle entre les rayons "rouges" qui émergent de la lentille et l'axe optique, soit l'angle ' de la figure. Ensuite, il suffit de savoir comment exprimer une tangente dans un triangle rectangle...

Merci beaucoup !

Je pense que cela devient plus clair...

Je vous avoue que je commence à paniquer car on est bientôt à la moitié des vacances et je n'ai pas du tout revu la moitié de la première année... Je ne serai jamais au point pour les concours...

Je vous envoie dans quelques minutes un dernier message avec mes dernières questions.

Dernières questions :

1. Je suis désolé, mais AB/f' cela ne correspond pas à la définition, ni au schéma, de l'extrait de cours ci-dessous... Je ne comprends pas ! Pourtant, oui, c'est la définition de la tangente... Mais AB c'est l'objet et non l'image ? Alors qu'on veut le diamètre apparent de l'image ?

2. Où est placé l'oeil ?

Merci, et désolé...

** image supprimée **

hum....

@malou :

mmalou @ 17-07-2019 à 19:20

hum....

malou, pourquoi avoir supprimé l'image ??!!

Et en plus vous vous plantez en disant que je fais du multipost...

Sympa de mettre des bâtons dans les roues aux élèves !

Bonsoir maalou : c'est exactement le même problème sur le plan mathématique mais pas du tout le même problème physique, quoique... en tenant compte du principe du retour inverse de la lumière...
Bonsoir etudiantilois : j'ai déjà répondu aux questions que tu poses dans ton message du 17-07-19 à 17:08...

Si vanoise vous pouviez m'aider à comprendre le lien entre le corrigé et cette définition...

Merci.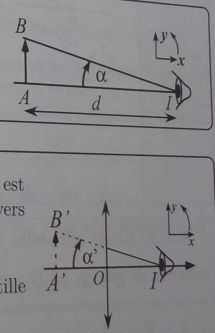


***image recadrée conformément au règlement***

@vanoise : nos messages se sont croisés...

Je ne suis vraiment pas sûr d'avoir compris...

Pourquoi écrire AB et non A'B' comme c'est le diamètre de l'image ?

Mais c'est vrai que A'B' est à l'infini donc on est coincé...

Autre question : pourquoi sur la figure on place l'image à l'infini à gauche en pointillé ? Pourquoi n'est-elle pas à droite ?

MERCI encore, et désolé...

Tu es tombé dans le piège (rassure-toi : tu n'es pas le premier !) : diamètre angulaire ou diamètre apparent ne désigne pas une distance comme le diamètre d'un cercle : il s'agit d'un angle. Plus cet angle est grand, plus l'image formée sur la rétine de l'œil est grande, plus il est facile de percevoir les détail de l'image.
On parle de diamètre angulaire si l'objet est regardé directement par l'œil ; on parle de diamètre angulaire apparent quand l'objet est regardé à travers un instrument d'optique (loupe comme ici, lunette, microscope...) ; dans ce cas, il s'agit de l'angle sous lequel l'image est vue à travers l'instrument. Dans le cas particulier où cette image est rejetée à l'infini, je t'ai expliqué de façon détaillée comment on définit le diamètre angulaire apparent.

Merci beaucoup, cela commence à être vraiment plus clair j'ai l'impression !

Mais ce n'est pas écrit dans le cours que j'ai joint dans mon message de 21h51 le cas où l'image est à l'infini ?

Alors comment aurait-on pu trouver la méthode que vous avez décrite seul ?

Merci encore pour le mal que vous vous donnez pour que je comprenne...

Le cas de l'image à l'infini correspond à la figure 4 de ton premier message et aux explications que j'ai fournies alors.

OK ! Mais, rassurez-moi (ou pas !), comment aurait-on pu trouver la formule A'B'/f' sans aide ?

A quoi servent les professeurs et accessoirement les forums d'aide ???
Plus sérieusement, ce n'est pas très difficile mais, j'en conviens volontiers, il faut un peu d'habitude pour s'en sortir... Pour vraiment bien comprendre, il faut savoir comment fonctionne l'œil : pour qu'il ne fatigue pas, il doit regarder des objets éloignés, en pratique à l'infini pour un œil normal. C'est pour cela que les instruments d'optiques (loupes, lunettes, microscopes...) sont destinés à donner d'un objet réel une image virtuelle rejetée à l'infini de plus grand diamètre angulaire apparent possible. C'est le cas de la loupe de la figure 4 de ton premier message.

Merci beaucoup !

Et y a-t-il d'autres choses à connaître de ce type en optique ?

Autre question : pourquoi l'image à l'infini est-elle en pointillé à gauche du signe de la lentille et pas à droite en traits continus ?

Merci beaucoup pour votre réponse.

C'est cela ce que je ne comprends pas :

"

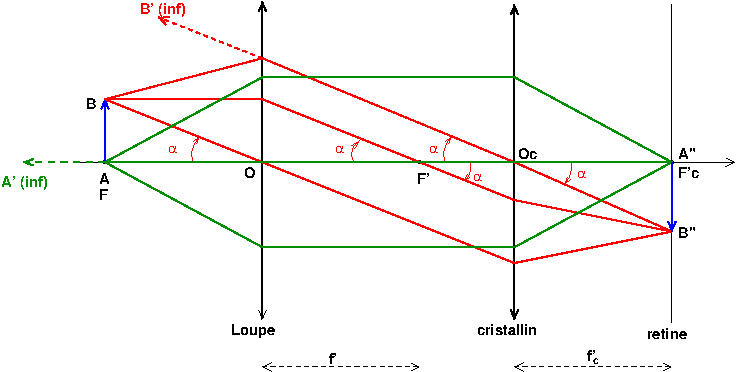
Pour t'aider à comprendre le fonctionnement de la loupe et plus généralement : comment l'œil peut voir un objet à l'infini, voici un schéma. Il reprend la figure 4 de ton premier message mais j'y ai ajouté l'œil schématisé de la façon suivante : une lentille convergente de centre Oc qui représente le cristallin et un écran : la rétine. Pour voir à l'infini, les muscles du cristallin font en sorte que la distance focale du cristallin f'_c soit égale à la distance entre le centre du cristallin et la rétine.
Ainsi, les rayons issus de A ( en vert) ressortent de la loupe parallèles à l'axe optique ; le cristallin les fait converger en son foyer image F'_c=A" : image de A par l'ensemble {loupe , cristallin}. Ainsi l'image d'un objet à l'infini sur l'axe optique se forme au foyer du cristallin. Les rayons issus de B ressortent de la lentille en un faisceaux de rayons parallèles entre eux inclinés par rapport à l'axe optique de '. Le cristallin les fait converger en B", image de B par l'ensemble  {loupe , cristallin} c'est à dire aussi image de B'(point à l'infini n'appartenant pas à l'axe optique) par le cristallin seul..
L'oeil voit donc distinctement un objet à l'infini. Un calcul très simple montre que la hauteur de l'image rétinienne est :
A"B"=f'_c.tan(').
Pour avir une image sur la rétine assez grande pour bien en distinguer les détails, il faut que l'objet à l'infini ait un diamètre angulaire apparent ' le plus grand possible.
PS : la police grecque de mon logiciel ne trace pas les accents. Sur mon schéma, il faudrait remplacer par '...