J'ai un petite problème pour résoudre cette exercice.

Les fabricants automobile ont trouve ́ des solutions pour detecter la presence d'eau sur le pare-brise d'une voiture. Un système de commande relie ́ a` un détecteur permet alors de déclencher les essuie-glaces automatiquement.
On modélise un pare-brise par une lame de verre a` faces parallèles d'épaisseur e = 5 mm et d'indice de refraction nv. Un rayon lumineux issu de l'émetteur E arrive sur le dioptre verre / air au point I avec un angle d'incidence i1. Le détecteur D est place ́ sur le pare-brise de fac ̧on a` recevoir le rayon lumineux lorsque le pare-brise est sec tel que |EI′| = |I′D|. L'air a un indice de refraction note ́ na. Lorsqu'il pleut, une lame d'eau d'indice de re ́fraction ne et d'épaisseur h = 1 mm, supposée constante, se depose sur le pare-brise.
Pour simplifier les calculs, on concèdera que les indices de refractions de l'air, de l'eau et du verre vérifient na =1,ne =√2et nv =√3,tel que na <ne <nv.

air
-----------------------------------------
eau                       i                                       hauteur h
------------------I-----------------------
verre                 / I\                                     hauteur e
                           /   I   \
                        /      I      \
------------/-----I-----\----------------------
                  E           i'          D        

1. Exprimer et calculer l'angle limite sur le dioptre verre / eau au-dela` duquel la reflexion est totale. Le rayon incident d'angle i1 = 45◦ se refracte-t-il dans l'eau ou se reflechit-il intégralement? Justifier votre réponse.
2. Determiner l'angle de refraction i2 au point I s'il existe.
3. Calculer la valeur de l'angle limite sur le dioptre eau / air pour avoir reflexion totale. S'il existe un rayon dans l'eau issu de E, se refracte-t-il dans l'air ou se reflechit-il ?
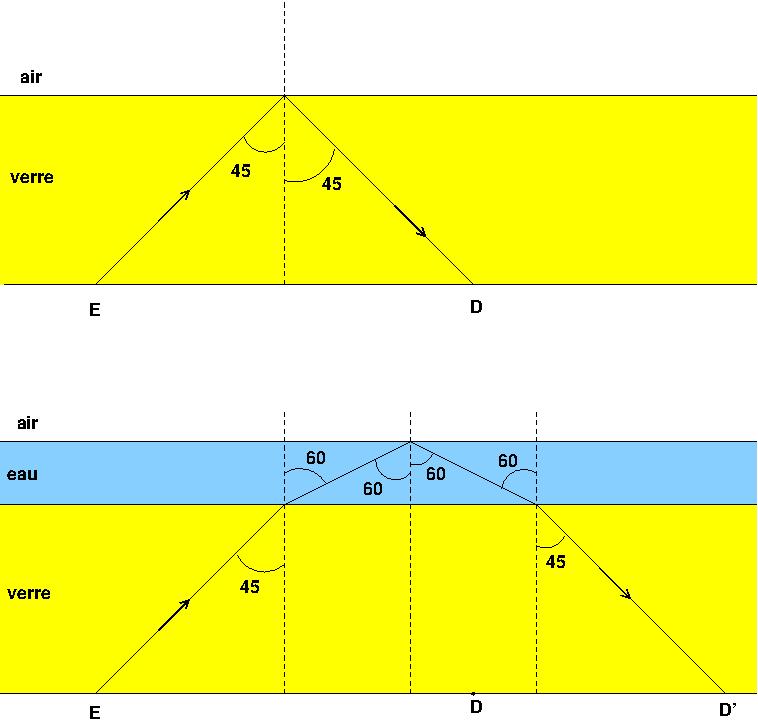
4. Repre ́senter, au propre sur votre copie, la propagation du rayon lumineux dans le cas ou` il pleut en y
faisant clairement apparaitre tous les angles pertinents.
5. Le de ́tecteur D qui intercepte le rayon lumineux lorsque le temps est sec, le rec ̧oit-il lorsqu'il pleut ? Si la réponse est non, a` quelle distance du détecteur arrive-t-il ?

Pour la question 1 .

-L'angle limite correspond au cas ou l'angle i vaut pi/2 dans la troisième loi de descartes.
n1sini(lim) = n2sin pi/2
on a donc n2sin pi/2 =1
on en déduit i(lim)= arsin n1/n2. ici n1= racine (2) et n2 = racine (3)
on a donc i(lim)= arsin racine (2) / racine (3) = 0,96 radian ou 54,7 degres

-On regarde si i1> i(lim) , si c'est le cas alors il n'existe pas de solution pour la 3eme loi de descartes, et la reflexion est totale.
ici i1+ 45 degrés et i(lim)= 54,7 degrés, on a donc i(lim)>i1 , le rayon incident va donc se réfracté dans l'eau.

Pour la question 2:
- On sait que n1 sini1 = n2 sini2
ici on cherche i2
sin i2= n1 sin i1 / n2
sin i2= 0,86
arsin i2 = 0,01
(je trouve ca petit pour un angle de refraction)

Pour la question 3 :
- on calcul i(lim)= arsin n2/n2 = arsin 1/ racine (2) =0,7 rad soit 40 degrés.
- un rayon issu de E va du verre dans l'air, il passe d'un milieu plus refringent  a un milieu moins refringent , il y aura un rayon réfracté et un rayon réfléchit , le rayon réfracté va se rapproché de la normale.

Pour la question 4
je n'arrive pas à dessiner correctement tout les rayons.

Pour la question 5
je n'arrive pas a résoudre le calcul.

Voila, merci pour votre aide!