Inscription / Connexion Nouveau Sujet
optique
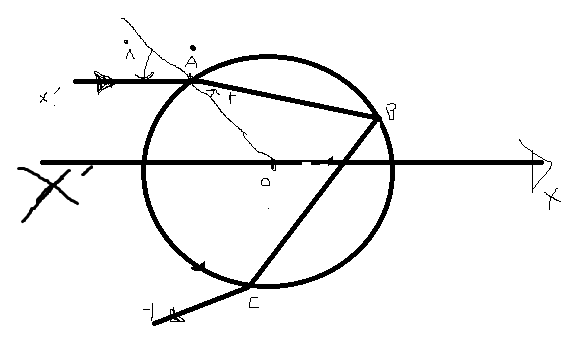
2. Dans un premier temps, on s'interesse au parcours des rayons du soleil dans une goutte d'eau modélisée par une sphère de centre O et de rayon R, qu'on supposera immobile dans l'air. Cette goutte est éclairée par un faisceau de lumière parallèle dont un rayon x'A atteint la sphère en A où il se réfracte. On pose (OA,Ax')=i et (AO,AB)=r, les angles d'incidence et de réfraction (figure 2). Soit B le point où le rayon réfracté rencontre la sphère. En B la lumière peut être soit réfractée soit réfléchie, mais on ne considère ici que le rayon réfléchi. Le rayon réfléchi en B rencontre de nouveau la sphère en C où il se réfracte selon Cy. On note α=(OX',Cy)
On note n l'indice de réfraction de la goutte d'eau et on prendra l'indice de l'air égal à 1.
Dans un premier temps, on suppose que la lumière incidente est monochromatique de longueur d'onde λ.
3.2 Montrer que α=4r-2i
Bonjour également,
Je ne voudrais surtout pas brûler la politesse à athrun, peut être parti dessiner sur Geogebra pour que la demonstration soit ... cristalline.
Donc pour mettre jonus sur la voie un petit peu:
dans le triangle ABC, l'angle B^ vaut 2r (car le triangle AOC est isocéle)
Donc de même dans le triangle OCB, l'angle C^ vaut r
Et si le rayon arrive avec une incidence r en C il ressort avec une incidence i (ie l'angle (CO,Cy) = i)
On s'en doutait un peu mais ça va mieux en l'écrivant
jonus, pour te mettre un peu plus avant sur la voie, tu places sur ton joli dessin un point D à l'intersection des droites Ax' et OB. L'angle 
apparait alors comme le nez au milieu de la figure (de Descartes d'ailleurs)
Quelques considérations sur les triangles AOB et AOD, devraient te permettre de conclure...
Bonjour PerArGal,
je ne suis pas parti dessiner quoi que ce soit, j'essayais d'apprendre la politesse à jonus qui manifestement nous prend pour ses chiens...
@athrun,
Tu as raison de souligner que je n'y fais même plus attention ... alors quelque part ... c'est tout de même un peu "gavant".
@jonus, tu n'as qu'un mot à dire et nous serons comblés!
Annuler
connectez vous