Merci à toute bonne âme

quel est ton raisonnement et qu'as tu trouvé?

En considérant que l'observateur se positionne à ras de l'eau à une distance d (depuis le centre du disque jusqu'au bord du bac)
sin i = n.sin r => r = 49°
tg r = d/h = 1.14 => d = 1.14.h = 5.7cm
Or R=10cm => ???

Voilà ce que j'ai trouvé, et cela ne me satisfait pas...

Pourrais-tu donner les données numérique?

n, h

Ca fait longtemps que je n'ai plus fait d'optique

Mais pour moi:

l'angle r est donné par les dimensions R et h

tan r = h/R => r=63,4°

sin i = n.sin r, avec n=1,33

on trouve que sin i = 1,19 : on ne peut pas donc pas voir l'extrémité.

A vérifier.

Est-ce que le fait que le disque soit d'épaisseur négligeable, on peut le supposer transparent sans impact sur le rayon incident, et de ce fait faire tout le raisonnement avec cette hypothèse?

si le disque était transparent, ce serait dit, on pourrait voir l'extrémité de partout, comme si le disque n'existait pas.

donc à mon avis il ne faut prendre comme hypothèse que le disque est transparent.

Bonjour a tous les deux,

puis-je vous aider ?

Pour Kboum : l'hypothese du disque transparent est evidemment a rejeter, ne serait-ce que parce qu'on peut realiser des surfaces opaques et de tres petite epaisseur. On suppose l'epaisseur du disque negligeable pour que les deux faces soient pratiquement confondues avec la surface de l'eau, tout simplement.
Lamat t'a demmande les valeurs numeriques de R et de h. J'ai l'impression que R vaut 10 cm et que h = 5 cm, mais il faudrait une confirmation. Si c'est bien ca, l'exercice est termine car l'observateur ne verra jamais la pointe A de la tige, quel que soit l'endroit ou il se place (voir le calcul de lamat qui est correct).

Prbebo.

Bonjour,
Merci pour l'intérêt que vous avez porté à cet exo...
Pour ce qui concerne les valeurs, celles que vous avez déduites sont les bonnes. Pourtant, comme c'est un exo d'annales de concours cela me laisse sur ma faim que l'on ne puisse pas voir la pointe A. En général, dans les concours il y a toujours une solution ou groupe de solutions. D'ailleurs, sur le site "chimix" ils proposent une solution qui a considéré entre autre la transparence du disque (dont voici le lien : http://www.chimix.com/an7/ing7/itpe41.htm ).

Bonne journée.

Bonjour a tous les deux,

Kboum, je viens de regarder le site dont tu m'as donne l'adresse ci-dessus. Une reaction a chaud : ce site est pourri, et un conseil : oublie-le tres vite !
Premiere anomalie : les rayons lumineux partent de l'air pour entrer dans l'eau, cad de l'oeil pour arriver en A. A part quelques ados qui croient que c'est l'oeil qui projette des rayons vers les objets pour les voir, tout le monde sait que c'est le contraire : l'oeil est un capteur, et un capteur c'est fait pour... capter, et non pour emettre.
Il ne s'agit pas d'un simple lapsus dans les schemas, car Mme Aurelie (celle qui signe dans le site) parle d'incidence rasante, alors qu'il s'agit au contraire de refraction rasante. Pas pareil ! Lamat, qu'en penses-tu ?

Deuxieme anomalie : la  distance d a partir de laquelle on peut voir ou ne pas voir le point A est une anerie. Si un rayon issu de A peut traverser la surface de l'eau et se retrouver dans l'air, meme en emergence rasante, alors l'oeil de l'observateur pourra capter ce rayon en se placant a n'importe quelle distance de O.

Je n'ai pas le temps de developper ma reponse maintenant, mais je vous promets de le faire ce soir, avec des schemas explicatifs.

A tout a l'heure,

Prbebo.

Je suis un peu en retard, mais me revoila.
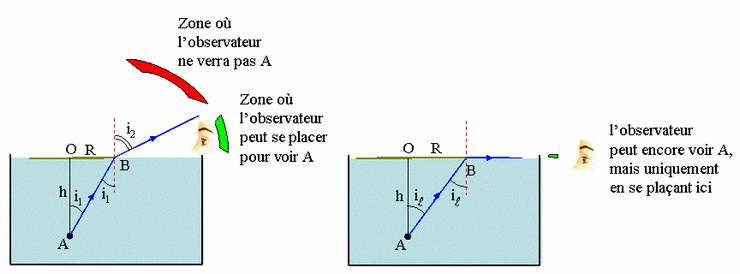
Regardez le premier schema ci-dessous, il represente un rayon issu de A et qui, apres avoir frole l'extremite B du disque, peut ressortir et se retrouver dans l'air. Pour ecrire les lois de Descartes, mieux vaut abandonner la notation sini = n.sinr, pour celle-ci : n1.sini1 = n2.sini2, ou l'indice 1 se refere au milieu incident (celui d'ou part le rayon incident) et l'indice 2 au milieu emergent. Ici, le milieu 2 est l'eau, donc n1 = n et i1 l'angle tel que tani1 = R/h, et n2 l'air (n2 = 1).
On se trouve dans le cas ou n2 < n1, donc le rayon emergent s'ecarte de la normale (i2 > i1) et est susceptible de ne pas traverser la surface de l'eau si l'angle i1 est trop eleve. La limite prise par i1 au-dela de laquelle le rayon ne sort pas de l'au et donc subit une reflecion totale est i_lim, tel que sini_lim >= 1/n (i2 >= /2). Avec n = 1.33, on trouve facilement i_lim = 49^o, soit tanil = 1.15.

On se place dans l'hypothese ou le disque est opaque.

1er cas de figure : R/h < 1.15 (cas de la figure 1) : le rayon AB traverse le dioptre plan et fait avec la normale l'angle i2 < /2. Si l'observateur se place dans la zone verte, il pourra capter ce rayon ainsi que tous ceux qui apres refraction se trouvent dans cette zone. L'observateur peut donc se placer n'importe ou dans cette zone, aussi loin de O qu'il le desire, et et en s'ecartant de la surface de l'eau pourvu qu'il reste en-dessous du rayon emergent correspondant a l'incident AB.
La distance entre l'oeil et le centre O du disque n'intervient donc pas.
Si on augmente le rapport R/h, par exemple en diminua la longueur h de la tige tout en maintenant constant le rayon R du disque, on augmente l'angle d'incidence i1, et donc l'angle d'emergence i2 : le rayon emergent se rapproche de la surface de l'eau et la zone verte diminue.

Cas limite ou i1 = i_lim : le refracte est tangent a la surfavce de l'eau et la zone verte se reduit a une seule direction : l'observateur doit placer son oeil au ras de l'eau pour capter l'ultime rayon pouvant emerger. Il ne peut plus s'elever au-dessus de la surface, en revanche il peut s'eloigner de O : la distance baptisee d n'intervient donc toujours pas.

Cas ou R et h sont tels que i1 > i_lim (ce qui se produit avec les valeurs numeriques R = 10 cm et h = 5 cm) :
Alors aucun rayon ne peut sortir de l'eau. L'observateur ne peut voir le point A.

cas du disque transparent :

Les deux situations decrites ci-dessus sont toujours la, mais de plus puisque le disque n'offre plus d'obstacle au passage de la lumiere tous les rayons issus de A et qui arrivent sur la surface en des points I places entre O et B [peuvent ressortir en traversant le disque (d'ailleurs, un disque transparent et d'epaisseur negligeable equivaut a... rien du tout ; autant l'enlever et ne considerer que le dioptre eau-air). On en conclut que l'observateur peut cette fois se placer n'importe ou au-dessus de l'eau : il captera toujours au moins un rayon issu de A.

Conclusion : la distance d demandee n'a aucun impact dans cet exercice.

Prbebo.

Bonjour à tous les deux,

pas de réaction sur mon interprétation de cet exerice ?

Prbebo.

Salut,

j'étais content que tu confirmes que mes calculs étaient justes, après que Kboum a apprécié tes explications ultra-détaillées.

Je ne suis pas allé sur le site indiqué par Kboum, je n'ai donc pas d'avis à donner. De plus je confirme que selon moi, si le disque est transparent; l'exercice n'a pas d'intérêt car:

si le disque était transparent, ce serait dit, on pourrait voir l'extrémité de partout, comme si le disque n'existait pas.

Nous sommes donc d'accord

iamat