Inscription / Connexion Nouveau Sujet
Onde ressort
Bonsoir.
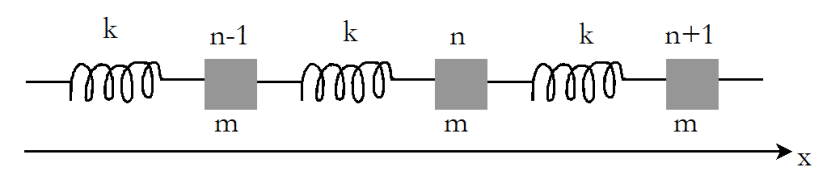
Je travaille sur les ondes longitudinales. Tous les exemples que j'ai pu voir pour les illustrer concernent soit un oscillateur avec une masse à l'une des extrémités, soit par exemple (ce qui se rapproche le plus de ma question), un ensemble de masses m identiques reliées entre elles par des ressorts de constante de raideur k (voir image 2).
Ainsi, dans ce dernier cas, en considérant que les masses(oscillateurs) sont distantes entre-elles de a, on aboutit à l'équation de d'Alembert :
.
On a dans ce cas . Avec
la masse linéique, on obtient
.
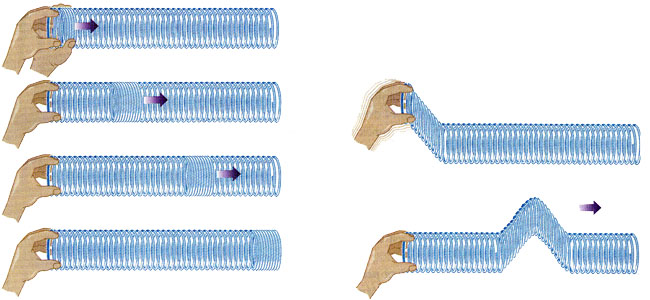
La question que je me pose concerne un ressort hélicoïdal tenu droit et horizontal (voir image 1 exemple de gauche).
Peut-on utiliser la même équation, en supposant alors que la distance a correspond à la distance entre deux points identiquement placés sur deux spires contigües?
Quelle distance a raisonnable pourrait-on alors prendre pour une application numérique?
Merci par avance pour vos indications.
Bonsoir,
Il y a effectivement des analogies entre le cas que tu viens d'étudier et la propagation d'ondes longitudinales le long d'un ressort (figure de gauche). Il faut appliquer la relation fondamentale de la dynamique à une tranche élémentaire de largeur au repos dx et de masse µ.dx. Tu devrais facilement trouver une démonstration sur internet ; cherche si cela t'intéresse puis pose éventuellement d'autres questions. En revanche, la figure de droite correspond à la propagation d'ondes transversales et la mise en équation est assez différentes.
Bonjour Vanoise, et merci infiniment pour ton aide.
Je me suis en effet emmêlée en essayant de réfléchir à partir des spires du ressort.
Pour suivre l'analogie relative au cas (ensemble de masses m reliées entre elles par des ressorts de même raideur) il faut en effet considérer le ressort de longueur L comme une association en série de N = L/dx petits ressorts en série et non pas comme je tentais, de raisonner vis à vis de deux spires contigües (séparées d'une distance a).
J'ai refait toute la démonstration pour aboutir à la conclusion .
Merci à nouveau et bonne fin de journée.
Bonsoir,
C'est effectivement cela ! Je pense que c'est seulement pas étourderie que la racine carrée est manquante.
j'étais pourtant sure d'avoir mis un \sqrt dans ma formule. Une erreur d'"orthographe" Latex sans doute.
Merci encore pour votre vigilance.
Salut,
pour une appli numérique il faut prendre groso modo 6 points par longueur d'onde.
Donc faut voir quelle est la fréquence max à laquelle tu travailles et en déduire la longueur d'onde correspondante. Diviser la longueur du ressort par la longueur d'onde et multiplier par 6.
Sinon, faut bien voir que l'équation d'onde présente une certaine généralité. Elle peut s'appliquer aussi bien au vibrations longitudinales, aux vibrations de torsion de poutres, aux cordes vibrantes et aux tuyaux sonores.
Seules les vibrations de flexions ne sont pas régies par cette équation (présence d'ondes évanescentes).


