Inscription / Connexion Nouveau Sujet
Norton
Bonjour,
j'ai des difficultés sur cette exercice, je dois calculer et dessiner les générateurs de Norton.
Merci

Bonjour
réseau 3 : il suffit de remplacer les deux résistance en dérivation par leur résistance équivalente.
réseau 4 : quasi identique à un exercice déjà proposé dans un message précédent...
réseau 3 : on te demande le générateur de Norton vu des bornes A et B. La résistance de Norton correspond donc à la résistance équivalente à R1 // R2. Le problème serait différent si les bornes A et B étaient décalées vers la gauche, entre les deux résistances...
réseau 4 : commence par remplacer le générateur linéaire de tension {E,R1} par le générateur linéaire de courant équivalent. Tu vas alors obtenir un circuit tout à fait analogue au réseau 3.
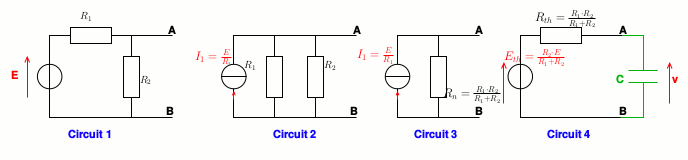
OK pour le réseau 3. Pour le réseau 4, les schémas ci-dessous devraient t'aider. La réponse attendue ici correspond au circuit 3.
remarque à titre d'approfondissement et seulement si tu as un peu de temps devant toi. Tu as peut-être remarqué que, dans l'exercice sur la charge du condensateur que tu as posté, le condensateur est précisément chargé par un ensemble {E,R1,R2} identique au réseau 4 de cet exercice. La solution qui t'a été présenté prends très logiquement le problème "à partir de zéro". Si par hasard l'étude de cette charge est à traiter à la suite de cet exercice, il est possible de remplacer le circuit de charge par le générateur de Thévenin équivalent au générateur de Norton. Cela correspond au circuit 4 ci-dessous. L'étude est alors très simple et correspond à celle que tu as sans doute traitée en cours. L'équation différentielle vérifiée par v devient très simple :
Avec pour solution pour t>0 :
La technique consistant à remplacer un générateur de Thévenin par son équivalent de Norton, regrouper de façon astucieuse les résistances pour revenir au final à un générateur de Thévenin est fréquemment utilisée pour simplifier les circuits...
Donc:
Pour le réseau 4, j'obtiens In=2/3V mais pourquoi Rn=12/8ohm et pas 8 (6+2)ohm
Pour le réseau 3, j'obtiens In=1/6V et Rn=2ohm
Ton message de 15h59 me rassure ! 
Tu as laissé ici les résultats sous forme de fractions. J'imagine que tu l'as fait exprès pour bien montrer la méthode de calcul que tu as utilisée. Il faut évidemment présenter le résultat sous forme décimal avec un nombre de chiffres significatifs adapté comme évoqué dans un précédent message.


