Inscription / Connexion Nouveau Sujet
mouvements de la terre et d'un satellite
Bonjour 
Je n'arrive pas à comprendre une partie dans le corrigé d'un problème de mécanique de MPSI.
voilà le problème:
on considère un satellite de masse m soumis à l'attraction gravitationnelle de la terre supposée sphérique, de centre O, de rayon et de masse
.
on admettera que et donc que la terre peut être considérée comme fixe.
on posera avec G la constante de gravitation universelle.
1) Donner l'expression de la force s'exerçant sur la satellite
Rep: tel que r la distance entre le satellite et le centre de la terre et
est le vecteur unitaire dirigé depuis le centre de la terre vers la satellite.
2) Montrer que la trajectoire du satellite par rapport à la terre est plane. On pourra faire l'étude en coordonnées cylindriques de vecteurs unitaires correspondants
avec
le vecteur unitaire orthogonal au plan de cette trajectoire.
Rep: on montre que le moment cinétique par rapport à O est constant (et ), et puisque le vecteur position est toujours orthogonal au moment cinétique donc le mouvement ce fait dans le plan défini par O, le vecteur position initial et la vitesse initiale .
3) L'accélération du satellite peut s'écrire sous la forme:
(formule de Binet) où L représente le moment cinétique par rapport à O du satellite. La trajectoire du satellite est une ellipse d'équation où p et e sont des constantes appelées respectivement paramètre et excentricité. L'axe polaire et l'axe focal sont confondus. Donner l'expression du paramètre p en fonction de L, k et m.
Rep:
La relation fondamentale de la dynamique projetée selon la direction radiale s'écrit:
(je pense qu'il fallait écrire au lieu de
)
c'est à dire:
(de même ici)
La solution de cette équation est la somme de la solution générale sans second membre: et d'une solution particulière
On choisi arbitrairement comme direction de référence des coordonnées polaires dans le plan du mouvemnt celle qui réalise . Cela revient à confondre l'axe polaire avec l'axe focal. Alors la trajectoire du satellite est définie par :
donc et dans le cas d'un satellite, la trajectoire est une ellipse d'excentricité
j'ai pas pu comprendre la partie en bleu  quelqu'un peut m'expliquer s'il vous plait?
quelqu'un peut m'expliquer s'il vous plait?
Bonjour
Si 1/r = A cos(O - Oo)
Alors le périgée a pour position angulaire Oo
On peut toujours tourner les axes d un angle -Oo de façon à ce que le périgée se trouve à  =0
=0
ce qui est plus simple géométriquement
aussi l'angle est définie comment? parce que on a besoin d'un référentiel (o, ox, oy, oz) pour dire que
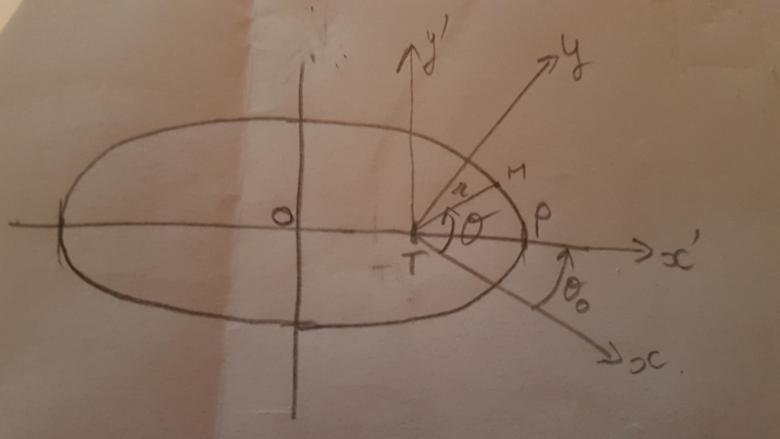
Il faut faire un dessin
Dans (T,x,y) on a pour trajectoire: r = p/(1+e cos(O-Oo) )
Le périgée P a pour position angulaire Oo
Si on tourne les axes et qu' on se place dans (T,x',y')
Alors r = p/(1+ e cos )
)
P a pour position angulaire 0 et  est compte à partir de l'axe Tx'
est compte à partir de l'axe Tx'