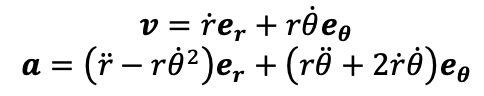Inscription / Connexion Nouveau Sujet
Mouvement spirale
Bonsoir je ne sais pas comment aborder le problème suivant :
Mouvement "spiral" d'un objet :
Un objet P de masse m est représenté en coordonnées polaires. Le mouvement de P est déterminé par la somme vectorielle des 2 forces extérieures qui agissent dessus (on néglige ici la gravité) :
F1 = -mk2r
F2 = -2mv avec 0 <
< k
F1 est une force similaire à celle d'un ressort (i.e. proportionnelle et opposée à l'élongation r), et F2 est une force de type frottement visqueux (i.e. proportionnelle et opposée à la vitesse v). On assume que
0,
et
0.
a) Ecrire les équations de mouvement à la forme différentielle sans les résoudre.
b) A partir des équations de mouvement, déterminer :
- la position r(t)
- l'angle (t), et déduire r(
) de r(t)
- la vitesse de l'objet v(t)
Données :
• Conditions initiales (à t = 0): = 0 et r = r0
• En coordonnées polaires la vitesse v et l'accélération a sont données par : image jointe
• La solution de l'équation = −
r est de type r(t) = r0 e
.
J'ai songé à faire que la somme des Fext = ma mais je ne m'y retrouve vraiment pas aves les coordonnées polaires et les points partout au-dessus des lettres et des angles. D'ailleurs les coordonnées fournies en pièce jointe sont-elles cylindriques et l'énoncé s'est trompé en disant qu'elles étaient polaires (sphériques) ?
Je vous prie de bien vouloir m'indiquer la marche à suivre svp
J'ai confondu polaires avec sphériques, donc si j'ai bien compris ce mouvement est étudié en 2 dimensions ?
Bonsoir
si j'ai bien compris ce mouvement est étudié en 2 dimensions
Oui : l'énoncé parle d'une spirale comme trajectoire et parle aussi de coordonnées polaires (pas cylindriques, pas sphériques...)
Il faut donc projeter la RFD suivant er et suivant e
 .
.
La première projection te donne une équation facile à résoudre qui va te fournir l'expression de r en fonction de t.
La seconde relation, une fois remplacés r et ses dérivées par rapport à t par les valeurs déduites de l'étude précédente, vont permettre d'obtenir l'angle
 en fonction de t.
en fonction de t.Je ne comprends pas ce que signifie "projeter la RFD suivant er et eteta". Auriez-vous une formule à me proposer ?
Tu écris l'expression vectorielle de la RFD puis tu identifies les termes en er et les termes en e . Tu as utilisé cette méthode dans l'enseignement secondaire avec les vecteurs unitaires (
. Tu as utilisé cette méthode dans l'enseignement secondaire avec les vecteurs unitaires ( ,
, ,
, )...
)...
Ton énoncé ne me semble pas complet : aucun renseignement n'est fourni concernant la vitesse initiale.
Je pense aussi que manquent d'autres renseignements...