Inscription / Connexion Nouveau Sujet
Mouvement Relatif 8.1
Bonjour,je voudrai de l'aide pour mon exercice que voici, c'est le schema que je veux d'abord avoir car je ne comprends pas la situation de l'exercice .Le voici:
Exercice:
Un plateau horizontal de centre O, d'axe Oz tourne autour de cet axe Oz à la vitesse angulaire ω constante par rapport au repère Oxyz lié au sol. Sur ce plateau on a tracé deux axes perpendiculaires Ox', Oy'. Un dispositif envoie une balle M suivant l'axe Oy à la vitesse vo.
A l'instant choisi comme origine des dates, les axes Ox', Oy' liés au plateau coïncident avec les axes Ox, Oy.
Exprimer les coordonnées (x', y') de la balle M dans le repère Ox'y'z' en fonction des coordonnées (x, y) de M dans le repère Oxyz.
Par rapport au référentiel lié au sol, le mouvement de la balle est rectiligne uniforme suivant Oy. Quelle est alors la trajectoire de M dans le référentiel lié au plateau.
Déterminer les composantes du vecteur vitesse et du vecteur accélération à tout instant t dans le repère lié au plateau.
Retrouver les résultats de la question 3 à partir des formules de composition des vitesses et des accélérations.
Merci 
!
Bonjour
Comme d'habitude : si tu commençais par poster un scan du schéma et par expliquer ce que tu as fait et ce qui te bloque ?
Ce schéma devrait t'aider. A toi de le compléter.
Le mouvement dans le repère fixe (O,x,y) est simplissime...
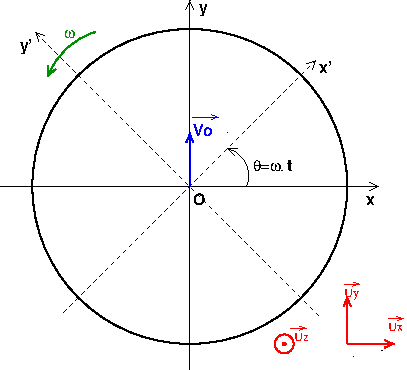
Oui; d'où la valeur de l'angle 
indiquée sur la figure. A ce repère R', on peut associer la base (U'x,U'y,Uz) comme indiqué sur la figure.
Le mouvement de M dans le repère fixe R est simplissime. Très facile d'exprimer alors le vecteur OM en fonction de Vo, t dans la base fixe (Ux,Uy,Uz).
Pour avoir les coordonnées x' et y' de M dans R' il suffit d'exprimer le vecteur unitaire Uy en fonction des vecteurs unitaires U'x et U'y.
En dérivant par rapport à t dans R' tu obtiens l'expression de la vitesse relative.
En dérivant une seconde fois par rapport à t dans R', tu obtiens l'accélération relative.
Il te reste alors à exprimer l'accélération d'entraînement et l'accélération de Coriolis puis à vérifier que la somme de ces trois accélérations fournit l'accélération dans R (accélération absolue).
PS : évidemment ici : l'accélération dans R s'obtient de façon évidente et directe mais tu es face à un exercice d'entraînement pour te familiariser avec ces notions.
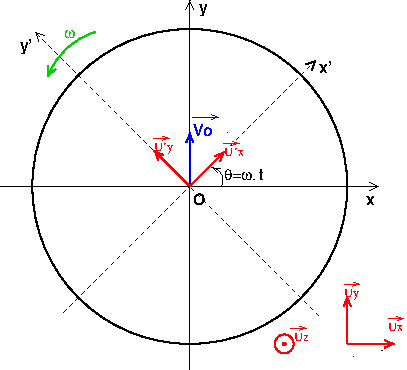
Tout est sorti 
mais par contre la derniere question je me demande bien comment avoir la vitesse absolue pour transposer et retrouver Vm/r' du 3
La vitesse absolue est fournie dans l'énoncé :
et donc, compte tenu de l'instant initial :
Une fois écrit le vecteur position sous la forme :
Tu obtiens la vitessse relative comme déjà indiqué :
Donc on a projete la vitesse absolue de M suivant les axes de R' seulement ? Si oui cela change t-il quelque chose, c'est-a-dire j'ai l'impression que c'est la vitesse relative qu'on a ?
Annuler
connectez vous