Inscription / Connexion Nouveau Sujet
mouvement relatif
Bonsoir, je cherche de l'ide pour cet exercice j'ai beaucoup de souci sur les mouvements relatifs. Merci d'avance:
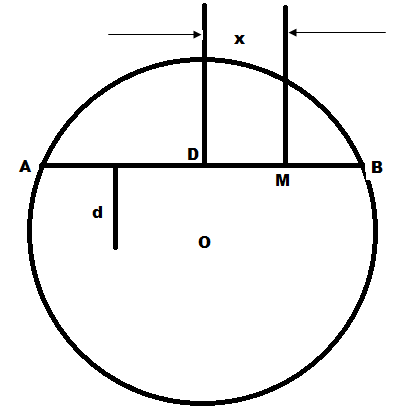
Un disque tourne autour d'un axe perpendiculaire à son plan et passant par son centre O avec une vitesse de rotation constante ω. Un point M se déplace sur la corde AB à partir de son milieu D avec une vitesse uniforme de module V0. La droite AB est parallèle au diamètre du disque et est située à une distance d du centre O.
1°/ Calculer la vitesse relative, la vitesse d'entrainement et déduire la vitesse absolue.
2°/ Calculer l'accélération absolue.
bonsoir,
la 1ère chose à faire dans ce genre d'exos est de bien définir les repères (origine + axes) :
- le repère fixe (R par ex.)
- le (ou les) repère "tournant" (R' par ex.)
D'après mon compréhension de l'exercice je peux prendre un repère R(O1,i,j) comme repère fixe et un repère R'(O,i,j) comme repère tournant d'où V0 représente relative.Est ce bon?
Hum Hum
Si R est fixe et R' tournant, comment peux tu avoir les memes vecteurs directeurs i et j dan sles deux repères?
Par ailleurs, il n'est dit nulle part que O était en mouvement. Donc pourquoi ne pas confondre O et O1?
Qu'en penses tu?
je peux prendre (O,i,j) comme repère R et (D;i',j') comme repère R'. Sinon soyez plus clair; comme je l'ai dit au début de mon message j'ai beucoup de souci sur les mouvements relatifs
je prendrais:
R (O, ,
, ,
, ) repère fixe
) repère fixe
R' (O, ,
, ,
, ) repère tournant lié au disque
) repère tournant lié au disque
 orientant la verticale (
orientant la verticale ( =
=  ^
^  )
)
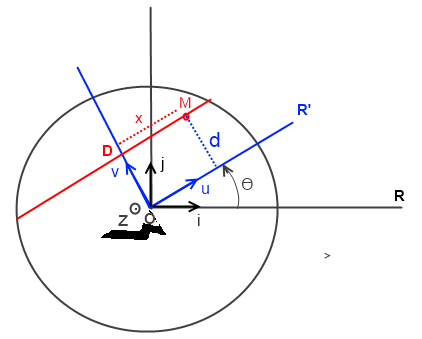
(cf figure)
Bonjour, comment déterminer maintenant la vitesse relative et la vitesse d'entrainement: je sais que la vitesse relative et la vitesse de M dans R' et je sais que V0 est parallèle au vecteur u.Mais je ne vois pas encore
je sais que la vitesse relative et la vitesse de M dans R' et je sais que V0 est parallèle au vecteur u.
oui, que veux-tu de plus ?
 (M) /R' = Vo
(M) /R' = Vo 
Ok maintenant pour déterminer la vitesse d'entrainement on a Ve= V(M)/R + Ω(R/R')Λ OM
mais comment déterminer Ω(R/R')
dans le cas de la rotation d'un solide autour d'un axe fixe, le vecteur instantané de rotation est:  =
= 

 étant le vecteur dir. de l'axe de rotation
étant le vecteur dir. de l'axe de rotation
et  la vitesse angulaire
la vitesse angulaire
(si la rotation est uniforme autour d'un axe fixe, alors  est un vecteur constant)
est un vecteur constant)
c'est à savoir
Rebonjour, je sas que OM=OD+DM mais comment donc calculer ce produit vectoriel c'est à dire : Ω Λ OD+DM (en grasse sont des vecteurs)
Ve= V(M)/R + Ω(R/R')Λ OM
non
Ve(M) est la vitesse par rapport à R, du point de R' coïncidant avec M
Je voudrais écrire Va = V(M)/R + Ω(R/R')Λ OM avec Va = vitesse absolue et Ve = vitesse d'entrainement
Ω Λ (OD+DM)
en fait tu veux dire:
V(M) /R = V(M) /R' +  (R'/R) ^ OM
(R'/R) ^ OM
Ve(M) =  ^ OM =
^ OM = 
 ^( x
^( x + d
+ d )
)
je te laisse développer le produit vectoriel
Voici mes calculs
Ve(M)=ωk Λ xu + ωk Λ dv = (ωx)k Λ u + (ωd)k Λ v =ωx+ωd
D'où Va=V0 u + (ωx)k Λ u + (ωd)k Λ v
D'accord donc finalement j'obtient Va = V0 u +(ωx)v - (ωd)u = (V0 - ωd)+ (ωx)u
Il me reste donc la question 2°/ Est ce que je peux dériver directement cette relation [(V0 - ωd)+ (ωx)u] car je sis que V0 est constante
oui, mais fais attention, les vecteurs  et
et  ne sont pas fixes
ne sont pas fixes
d'autre part on connait x en fct de Vo et de t
oui et comme u et v sont liés à R' on a:
d /dt =
/dt =  ^
^
d /dt =
/dt =  ^
^
donc tu trouves finalement a en fct de u et v
et tu peux vérifier la composition des accélérations:
 a =
a =  r +
r +  e +
e +  c
c


