Inscription / Connexion Nouveau Sujet
Mouvement rectiligne compliqué
***Bonjour***
soient deux astres, de formes sphérique ( ananas: diamètre: 12 756 km; masse:; ananas: diamètre: 3 474,8 km; masse:
) leurs centre de gravité
et
sont distants de 384 402 km. durant cette étude, je considère que nos deux astres sont isolés dans l'espace intersidéral, et constituent un système qui ne subit aucune contrainte de l'extérieur. compte tenu que les ananasiens considèrent que c'est orange qui depuis le debut de cette étude est en train de tomber sur eux, et en considérant la lois de l'attraction universelle;
1. déterminer la force ananas exerce sur orange au début de la chute;
2. déterminer cette même force lors de la collision des deux écorces;
3. après comparaison des deux résultats précédants, que peut-on dire de l'accelération de en application la RFD?
***Forum changé***
Bonjour,
Déjà, il y a une confusion dans ton énoncé, puisque les deux astres ont le même nom.
Ensuite, que proposes-tu ? La question 1. est une question niveau lycée.

bonjour, gbm.
je m'excuse pour la confusion, mais le deuxième astre s'appelle orange.
puis, je reviendrai pour la proposition, manque de temps. je te présente mes excuses au passage.
en fait, 384402km, c'est la distance initiale minimale entre les écorces.
mais, je me demande ce qu'est devenu la constante gravitationnelle que j'avais postée dans mon message originel. et comme promis, voici mes propositions et ma réelle préoccupation après:
1.
2.
3. avec 
, d'après la RFD,
; donc,

. en plus, cette variation me paraît régulière durant la chute, puisqu'elle dépend de la distance entre les centres de gravité des astres. or, aussi loin que je me souvienne, pour le mouvement rectiligne le plus complexe que j'ais étudié en mécanique classique, ( mouvement rectiligne uniformément varié), l'accélération demeure constante.
je vous demande alors, à vous qui êtes certainement plus avisés en mécanique que moi, quelle est la dynamique de ce genre de mouvement, que j'avais d'abord pris pour une ( simple ) chute libre, et donc, un mouvement rectiligne uniformément varié. merci de me répondre!
de shakageniesse, on est ensemble. 
bonjour,
la plupart des calculs de chute libre faits au lycée supposent que le champ de pesanteur (g) est uniforme ce qui n'est justifié que dans certains cas, par ex. lors de "petits" mouvements au voisinage de la surface d'une planete.
Dans cet exercice, le champ de pesanteur n'est pas du tout uniforme, g=g(r)
ce qui fait que le mouvement étudié est accéléré mais l'accélération n'est pas constante
Enfin, l'étude rigoureuse du mouvement de deux astres (composant un système isolé) est un problème très général, appelé le "problème à deux corps" et abordé en 1er cycle
bonjour à tous, j'ai lu un article concernant le problème à deux corps, ![]() . mais, personnellement, j'ai dressé le suivant tableau pour répondre à la question de la dynamique et la cinématique de ce mouvement.
. mais, personnellement, j'ai dressé le suivant tableau pour répondre à la question de la dynamique et la cinématique de ce mouvement.
| grandeurs | accélération du troisième ordre accélération | |||
| accélération d'ordre zerro (position) | ||||
| accélération du premier ordre vitesse |
Bonsoir
Vous avez déjà répondu dans votre 3e message à la question qui était posée: L'accélération n'est pas constante
Le seul problème c'est que vous avez appliqué le pfd dans un referentiel non galileen
Dans cet exo c'est pas trop grave, mais dans le cas d étoiles doubles par ex , ça serait totalement faux
C'est tout ce que je voulais dire dans mon message precedent
Bonsoir à tous!
Excuez mon ignorance, mais, j'aimerais savoir pourquoi pour krinn, le référentiel ici ne peut en aucun cas être galiléen.
Le seul problème c'est que vous avez appliqué le pfd dans un referentiel non galileen
Le référentiel lié à la terre (alias ananas) n est pas galileen car le rapport des masses des deux astres est ici de 1:80
Donc on ne peut plus vraiment écrire morange << mananas
Donc le centre de gravité de l'ensemble n'est pas confondu avec le centre de la terre
Le bon référentiel est le référentiel barycentrique qui ,ici, n'est pas confondu avec le réf. geocentrique, en toute rigueur
Bonjour,
Le bon référentiel est le référentiel barycentrique qui ,ici, n'est pas confondu avec le réf.
c'est lui que j'avais choisi.
Bonjour,
Le bon référentiel est le référentiel barycentrique qui ,ici, n'est pas confondu avec le réf. geocentrique, en toute rigueur
c'est lui que j'avais choisi plutôt.
Désolé alors pour cette meprise,
l enonce est très ambigu et j'ai cru que vous aviez pris le référentiel terrestre
Dans l'article ci-dessus, il se dégage plutôt, comme une rupture, par rapport aux mouvements étudiés au secondaire. Et pour rétablir l'équilibre, j'ai méné ume étude théorique, concernant le mouvement à deux corps, et les résultats sont condensées dans le tableau ci-dessous:
| Grandeurs | formules | unités |
| accélérarion d'ordre 0 (position) | m ( mère) | |
|
accélérarion du premier ordre ( vitesse ) | m.s^{-1} ( mère par seconde ) | |
|
accélérarion du deuxième ordre ( accélération ) | m.s^{-2} ou N/Kg, N. Kg^-1( mère par seconde carrée) | |
|
accélérarion du deuxième ordre ( accélération ) | m.s^{-2} ou N/Kg, N. Kg^-1( mère par seconde carrée) |
accélérationdu troisième ordre |
| m.s^{-3} ( mère par seconde cube ) tu |
Bonsoir
En définissant  comme la dérivée de l'accélération "a" par rapport au temps, la dimension physique de
comme la dérivée de l'accélération "a" par rapport au temps, la dimension physique de  est :
est :
[ ]=L.T-3 (mesure en m/s3)
]=L.T-3 (mesure en m/s3)
comme tu l'as écris.
Recherchons maintenant la dimension physique de
Une force correspond au produit d'une masse par une accélération :
[F]=M.L.T-2
se mesure en kg-2.s-2
Je te laisse conclure...
Le problème à deux corps, dans le cas particulier d'un mouvement rectiligne, conduit à une distance r entre les centres des deux astres vérifiant une équation différentielle de la forme :
Dans ce cas, la dérivée de l'accélération par rapport au temps n'est pas constante.
Oubli d'un signe "moins" dans l'exposant de T mais cela ne change pas fondamentalement la cohérence du message. Je rectifie néanmoins :
|
accélérationdu troisième ordre |
| m.s^{-3} ( mère par seconde cube ) vous comprendrez pourquoi la seconde unité de |
Merci à tous !
Bonjour à tous, voici la dernière ligne originelle de mon tableau:
|
accélérationdu troisième ordre |
| m.s^{-3} ( mère par seconde cube ) vous comprendrez pourquoi la seconde unité de |
Merci à tous !
Bonjour
J'ai essayé d'être diplomate est je n'ai manifestement pas été compris ; je vais donc me montrer plus direct...
Le fait que  et
et soient deux grandeurs de dimensions physiques différentes interdit toute comparaison entre ces deux grandeurs et encore plus l'égalité de ces deux grandeurs. C'est un peu comme si tu affirmais qu'une longueur puisse être égale à une masse !
Si , l'intégration de cette relation couplée à la RFD conduit à :
La force est ainsi fonction affine du temps. Je ne vois pas trop de situations réelles correspondant à cette situation...
La force est ainsi fonction affine du temps. Je ne vois pas trop de situations réelles correspondant à cette situation...
1. déterminer la force qu'ananas exerce sur orange au début de la chute;
2. déterminer cette même force lors de la collision des deux écorces;
3. après comparaison des deux résultats précédants, que peut-on dire de l'accelération de G_{O}
je crois que c'est justement le cas du problème à deux corps non
Non !
Dans le cas du problème à deux corps, étudié dans le référentiel barycentrique supposé galiléen, avec les conditions initiales de ce problème, la distance r entre les centres des deux astres vérifie l'équation différentielle :
L'accélération
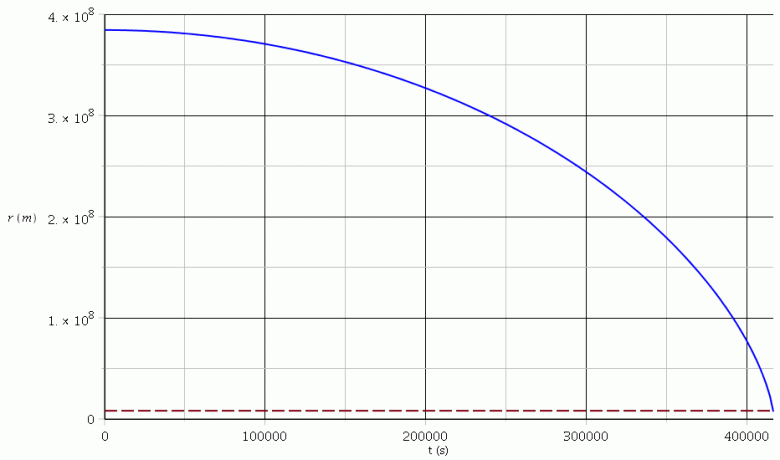
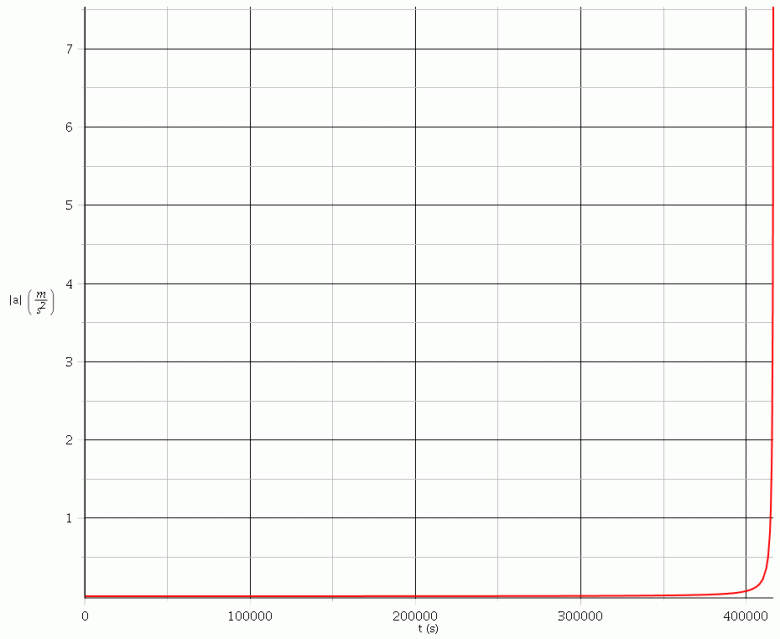
Pour illustrer à quel point la situation étudiée ici est éloignée d'une accélération fonction affine du temps, voici deux simulations informatiques utilisant les valeurs numériques et les hypothèses fournis dans le premier message de shakageniesse :
La première courbe (bleue) correspond à l'évolution au cours du temps de r (la ligne pointillée horizontale correspond à la valeur de r lors de la collision).
La seconde courbe (en rouge) correspond à l'évolution au cours du temps de la valeur absolue de l'accélération. On remarque que celle-ci augmente d'abord très lentement tant que les astres sont très éloignés pour augmenter très rapidement peu avant la collision.