Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Mouvement parabolique d'une balle

Posté par
tintin22 05-10-21 à 17:38

.Bonjour, j'ai cet exercice à faire,  mais je bug à partir de la 4ème question pouvez-vous m'aider s'il vous plaît?

Une balle de masse m assimilée à un point
matériel est lancée vers le haut à partir d'un
point O depuis le sol avec une vitesse initiale
\vec{v_0} dans le plan (xOy), de norme ||\vec{v_0}||
et faisant un angle α avec l'horizontale Ox. On
fera l'étude du mouvement dans un repère
(O, \vec{i} , \vec{j} ), en négligeant les frottements. La
figure 1 est obtenue expérimentalement à partir d'une chronophotographie de la trajectoire de la balle.

1. Exprimer les composantes v0x (selon \vec{i} ) et v0y (selon \vec{j} ) de la vitesse  \vec{v_0} au point
O dans le repère (O, \vec{i} , \vec{j} ), en fonction de sa norme ||\vec{v_0}||, que l'on notera pour
simplifier V0, et de l'angle α.

Alors v0x= V0cos α et v0y= V0sin α


2. Sachant que l'accélération vaut\vec{a} = −g\vec{j}(où g = 9, 81 m.s−2
), et en tenant compte
de la vitesse et de la position à l'instant t = 0 au point O, déterminer, dans le repère
(O, \vec{i} , \vec{j} ) :
— les composantes de l'accélération ax(t) et ay(t),
— les composantes de la vitesse vx(t) et vy(t),
— les composantes de la position x(t) et y(t).
On présentera les réponses sous la forme :
ax(t) = 0
ay(t) = -g
vx(t) = V0cos α
vy(t) = V0sin α  
x(t) = V0tcos α  
y(t) = - \frac{1}{2} gt² + V_0t\sin \alpha

3. En combinant les équations pour x(t) et y(t) pour faire disparaître le temps t, déterminer
l'équation y(x) de la trajectoire. Est-ce en accord avec la trajectoire expérimentale de
la figure 1 ? Justifiez votre réponse.

Au final en remplaçant g par  9.81 m.s-2,

on y(x) = \frac{-4.905x²}{V_0²cos²\alpha  } + x \tan \alpha
Donc la trajectoire expérimentale correspond, car on voit un polynôme du second degré avec un a négatif, donc la parabole aura un maximum.

4. Choisir une échelle pour les vecteurs vitesse, et représenter sur la figure 1 le vecteur
vitesse \vec{v} ainsi que ses composantes vx et vy aux points O, A, B, C et D en respectant
l'échelle choisie.

Alors à cette question, je sais pas quoi prendre comme échelle pour le vecteur
vitesse \vec{v} par contre pour ses composantes je dirai que  vx = \vec {i} et que vy = [tex]\vec{j}[\tex]. Après je sais donc tracer les composantes mais pas le vecteur vitesse.

5. La hauteur maximale atteinte par la balle est h au point B et à l'instant tB. Quelle est la vitesse [tex]\vec{v_B} de la balle au point B ? Exprimer tB et les coordonnées (xB, h) du
point B en fonction des données du problème.

Je publie dans un commentaire la suite car je crois que j'ai mis trop d'écriture LaTex

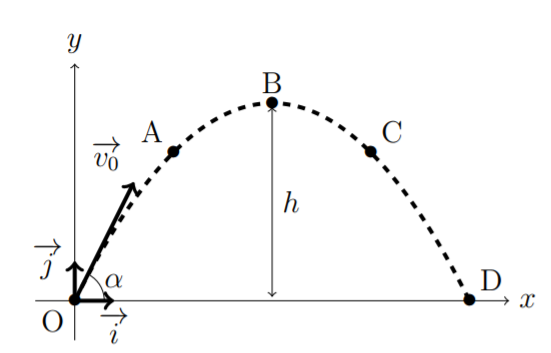
Mouvement parabolique d\'une balle

Posté par
tintin22re : Mouvement parabolique d'une balle 05-10-21 à 17:44

Alors je sais que le point B est donc au milieu du segment OD mais je vois pas comment exprimer tB et les coordonnées (xB, h).

6. La balle atteint le sol au point D à l'instant tD. Exprimer tD puis la distance OD.
Exprimer les composantes vxD
et vyD de la vitesse au point D, en déduire la norme
de \vec{v_D}.
7. Pour quel angle α la distance OD, c'est-`a-dire la portée, est-elle maximale ?

Étant bloqué avant je n'ai pas encore réfléchi a ces deux dernières questions. Je sais que l'exercice est long.
Je remercie d'avance celles et ceux qui voudront bien m'aider.

Posté par
vanoisere : Mouvement parabolique d'une balle 05-10-21 à 18:50

Bonjour
A la première question, tu as une erreur dans l'expression de vy(t).
Je te laisse corriger. Pour la suite, on peux remarquer qu'en B, vy(t) = 0.

Posté par
tintin22re : Mouvement parabolique d'une balle 05-10-21 à 20:05

Oui bien sûr, vy(t) = -gt + V0sin

Donc si en B, vy(t), cela veut dire que le vecteur vitesse \vec{v} =  vx(t) + 0 ? Soit V0tcos
Donc tB = \frac{\vec{v}}{V_0\cos \alpha}
me suis-je tromper?

Posté par
vanoisere : Mouvement parabolique d'une balle 05-10-21 à 20:17

Revois bien ton cours sur le sujet ; de façon générale :

v_{x}=a_{x}.t+v_{xo} \\ \\ v_{y}=a_{y}.t+v_{yo} \\ \\ x=\frac{1}{2}a_{x}.t^{2}+v_{ox}.t+x_{o} \\ \\ y=\frac{1}{2}a_{y}.t^{2}+v_{oy}.t+y_{o}

Posté par
tintin22re : Mouvement parabolique d'une balle 05-10-21 à 21:09

Comme vous venez de me le conseillez, j'ai relu mon cours, et je ne comprends donc pas où est mon erreur. Dans l'équation que vous me donner mon accélération vaut g même -g, Dans mon cours, on nous donne les équations des constante de a, de v et de x et y, et mes constantes correspondent donc avec mon cours. Donc je ne vois vraiment pas mon erreur au niveau de cette question. Pourriez-vous me l'expliquer s'il vous plaît?

Posté par
vanoisere : Mouvement parabolique d'une balle 05-10-21 à 21:11

Ici, compte tenu de l'expression du vecteur accélération :
ax = 0
ay = -g

Posté par
tintin22re : Mouvement parabolique d'une balle 05-10-21 à 21:20

Oui c'est ce que j' ai écrit en réponse à la seconde question,
ensuite
vx = V0cos\alpha
vy = -gt + V0sin\alpha

et donc
x =  V0tcos\alpha + x0 or x0 = 0
y= -\frac{1}{2}gt² + V0tsin\alpha + y0 or y0 = 0

Posté par
vanoisere : Mouvement parabolique d'une balle 05-10-21 à 22:22

Ok. Tu es parti sur de bonnes bases  maintenant.

Posté par
tintin22re : Mouvement parabolique d'une balle 05-10-21 à 22:43

C'est ce que j'ai écrit depuis le début…
Je suis un peu perdu là

Posté par
vanoisere : Mouvement parabolique d'une balle 05-10-21 à 23:22

Citation :
Donc si en B, vy(t), cela veut dire que le vecteur vitesse \vec{v} =  vx(t) + 0 ? Soit V0tcos
Donc tB = \frac{\vec{v}}{V_0\cos \alpha}
me suis-je tromper?


v_{y(t)}=-g.t+V_{o}.\sin\left(\alpha\right)

donc :

t_{B}=\dfrac{V_{o}.\sin\left(\alpha\right)}{g}

Ce n'est pas ce que tu as écrit dans ton message de 20h05.

Posté par
tintin22re : Mouvement parabolique d'une balle 06-10-21 à 07:23

Or on peut voir qu'au point B la constante vy(t) = 0 car B est le sommet, donc tB ne peut donc pas s'écrire en fonction de vy(t) , c'est pour cela que je suis passé par le vecteur vitesse qui est égale à la somme de ses constantes.
Soit \vec{v} = vx + vy
\vec{v} = V0tcos\alpha + 0
t = \frac{\vec{v}}{V_0cos \alpha}

Posté par
vanoisere : Mouvement parabolique d'une balle 06-10-21 à 08:38

Ton dernier message est faux : tu oublies les vecteurs unitaires dans l'expression du vecteur vitesse.
Ensuite  : vu est nul seulement au sommet de la trajectoire, c'est à dire à la date tB, pas à une date t quelconque.
Enfin : t est un nombre réel : il ne peut pas être égal à un vecteur divisé par un nombre réel...
Relis mon message précédent et revois au besoin ton cours sur les vecteurs en maths.

Posté par
tintin22re : Mouvement parabolique d'une balle 06-10-21 à 10:42

D'accord c'est parce que vy(t) = 0 qu'on peut trouver tB alors que moi j'ai mélanger avec les coordonnées du vecteur vitesse, qui serait \vec{v} = (vx\vec{i}, 0\vec{j})

Posté par
tintin22re : Mouvement parabolique d'une balle 06-10-21 à 10:51

et donc la vitesse \vec{v_B} = \sqrt{v_x²+0²}

\vec{v_B} = \sqrt{(V_0t\cos\alpha)²}

\vec{v_B} = V0tcos\alpha

Posté par
vanoisere : Mouvement parabolique d'une balle 06-10-21 à 13:13

Encore une fois : un vecteur ne peut pas être égal à un scalaire ! Tu risques d'être lourdement sanctionné un jours d'examen ou de concours si tu ne te montres pas plus rigoureux dans tes notations.
Au sommet B : puisque vyB=0 :

\overrightarrow{v_{B}}=v_{xB}.\overrightarrow{i}
Le vecteur vitesse est à chaque instant tangent à la trajectoire ; il est donc logiquement horizontal au sommet de celle-ci.

La valeur algébrique de la vitesse en B est ainsi :

v_{B}=v_{xB}=V_{o}.\cos\left(\alpha\right).t_{B}=V_{o}.\cos\left(\alpha\right)\cdot\dfrac{V_{o}.\sin\left(\alpha\right)}{g}

Je te laisse simplifier...

Posté par
tintin22re : Mouvement parabolique d'une balle 06-10-21 à 14:26

Oui je vous remercie, je vais tacher de faire plus attention.
Nous sommes a la question 5)
On a définit tB, vB,
Il ne manque plus qu'à exprimer les coordonnées de B en fonction des données du problème.

Alors on sait que B = (xB, h)
On utile les composantes de la position avec tB
Soit x(tB) = V_0\cos \alpha*\frac{V_0\sin(\alpha)}{g} on simplifie soit \frac {V_0 ²\sin 2\alpha}{2g}

et y(tB) = -\frac{1}{2}g(\frac{V_0 \sin \alpha)²}{g} +V_0 \sin \alpha \frac{V_0 \sin \alpha}{g}

= -\frac{V_0 ²g\sin²\alpha}{g²}+ \frac{V_0 ²\sin²\alpha}{g}

On a donc calculer les coordonnées du point B, si je n'ai pas fait d'erreur....

Posté par
vanoisere : Mouvement parabolique d'une balle 06-10-21 à 14:45

Désolé j'ai écrit quelque chose de faux dans mon précédent message.Je reprends.
La composante de la vitesse suivant x est une constante.

\overrightarrow{v_{B}}=v_{xB}.\overrightarrow{i}=V_{o}.\cos\left(\alpha\right).\overrightarrow{i}
Pour avoir les coordonnées du point B, il suffit de remplacer t par tB dans les expressions de x et y. C'est ce que tu as fait mais il y a une étourderie de calcul dans l'expression de yB à la dernière ligne.

Posté par
tintin22re : Mouvement parabolique d'une balle 06-10-21 à 15:00

D'accord je vous remercie je vais regarder où est mon erreur,

Pour la question 6) on utilise le même procédé sauf qu'au lieu que se soit la composante vy qui soit égale à zéro, se sera vx donc on calcule tD par grâce  à vx.
La distance OD est égale à l'abscisse de D,
on remplace t par tD dans vy, vx = 0

Et la norme du vecteur \vec{v_D} = \sqrt{v_x ².\vec{i}+ v_y ².\vec{j}}
Or vx = 0 donc
\vec{v_D} = \sqrt{v_y ².\vec{j}}

C'est cela?

Posté par
vanoisere : Mouvement parabolique d'une balle 06-10-21 à 15:14

Cd reste constant et n'est donc pas nulle en D.
Il faut commencer par exprimer tD en considérant yD=0 puis remplacer t par tD dans les expressions de vy et de x.

Posté par
tintin22re : Mouvement parabolique d'une balle 06-10-21 à 15:24

Donc tD  =  \frac {V_0 \sin \alpha}{g} ?

Posté par
vanoisere : Mouvement parabolique d'une balle 06-10-21 à 16:02

Non. Relis mon message précédent...

Posté par
tintin22re : Mouvement parabolique d'une balle 06-10-21 à 16:59

Doit on calculer le discriminant Delta soit b²-ac ?
Si oui
yD = -\frac{1}{2}gt_D ²+V_0 \sin (\alpha)t_D

Donc a = -\frac{g}{2}[\tex] \\ b = [tex]V_0 \sin (\alpha)
c = 0
Delta = (V_0 \sin (\alpha))²
et après on donne les racines
1ère racine = \frac{-(V_0 \sin (\alpha))-\sqrt{(V_0 \sin (\alpha))²}}{-\frac{g}{2}}
la seconde = \frac{-(V_0 \sin (\alpha))+\sqrt{(V_0 \sin (\alpha))²}}{-\frac{g}{2}}

Après simplification 1ère racine  = \frac {4(V_0\sin \alpha)}{g}

la seconde = 0 donc tD = \frac {4(V_0\sin \alpha)}{g}

Sinon je ne vois vraiment pas comment faire...
Je vous remercie vraiment de votre aide

Posté par
vanoisere : Mouvement parabolique d'une balle 06-10-21 à 19:59

Tu te compliques énormément la vie. La mise en facteur de tD évite de calculer le discriminant.

y_{D}=-\frac{1}{2}gt_{D}{{}^2}+V_{0}\sin(\alpha)t_{D}=t_{D}\cdot\left[-\frac{1}{2}gt_{D}+V_{0}\sin(\alpha)\right]=0

puisque tD 0 , le résultat est simple. Il est intéressant de comparer tB à tD.

Posté par
tintin22re : Mouvement parabolique d'une balle 06-10-21 à 21:09

Désolé je vais paraître bête mais je ne comprends vraiment pas ce qu'il faut faire pour isoler tD, la seule chose que je pense et que  tD = 2tB puisque que B est le sommet de la parabole et D une des racines...

Posté par
tintin22re : Mouvement parabolique d'une balle 06-10-21 à 21:13

J'ai une question même si je me suis compliqué la vie en calculant le discriminant, mon raisonnement était-il juste?

Posté par
vanoisere : Mouvement parabolique d'une balle 06-10-21 à 23:28

Suppose qu'en cours de math, on te demande de factoriser un polynôme et que tu obtiennes :
P(x)=x.(x-a) où a est un nombre réel.
Quelles sont les deux valeurs possibles de x telles que P(x)= 0 ?
Surtout ne pas développer et calculer un discriminant ! Le résultat est immédiat !
En appliquant la méthode à ce problème de physique, tu vas effectivement vérifier :
tD = 2tB .

Posté par
tintin22re : Mouvement parabolique d'une balle 07-10-21 à 07:55

D'accord donc mon raisonnement par rapport au graphique était juste du coup.
Donc si tt_D = 2t_B
alors
v_xD= 2t_B V_0 \cos \alpha
v_yD = -2gt_B + V_0 sin \alpha

Donc ||\vec{v}|| = \sqrt{v_xD + v_yD
= \sqrt{(2t_B V_0 \cos \alpha)² + (-2gt_B + V_0 sin \alpha)²

=\sqrt{4t_B ²V_0 ² \cos² \alpha + 4g²t_B ²- 4gt_B V_0 \sin \alpha + V_0 ² \sin² \alpha}

Apres je ne vois pas comment simplifier plus a part en factorisant par 4 ...

Posté par
vanoisere : Mouvement parabolique d'une balle 07-10-21 à 14:13

Même erreur que précédemment concernant vx. Puisque ax=0, vx=constante=Vo.cos() ; cela s'applique aussi bien en B qu'en D.

Posté par
tintin22re : Mouvement parabolique d'une balle 07-10-21 à 15:02

D'accord donc  
v_xD = V_0 \cos \alpha car a_D = constante
v_yD = -2gt_B + V_0 \sin \alpha

v_D = \sqrt{V_0 ² \cos²\alpha+4g²t_B ²+ V_0 ² \sin²\alpha}
ON factorise par V0
v_D = \sqrt{V_0 ²(cos²\alpha\sin²\alpha)+ 4g²t_B²}
v_D = \sqrt{V_0 ²*1+ 4g²t_B²}
v_D =V_0 + 2gt_B}

Question 7: Pour quel angle \alpha la distance OD, c'est-à-dire la portée, est-elle maximale ? Alors pour cette question intuitivement je dirais que l'angle doit être <= 45° mais doit être > 0°. En réalité je ne vois pas comment faire pour trouver une solution... Pouvais-vu m'aider?

Posté par
vanoisere : Mouvement parabolique d'une balle 07-10-21 à 16:16

vxD=Vo.cos() car ax = 0 (pas une constante quelconque)
Enorme erreur de math lors du passage de l'avant dernière à la dernière de tes formules. Dans le calcul, avant de le simplifier, il faut remplacer tB par son expression en fonction de g, Vo et .

Posté par
tintin22re : Mouvement parabolique d'une balle 07-10-21 à 16:30

Donc
v_xD =\sqrt {V_0 ² + 4g² \frac{V_0 ²\sin² \alpha}{g²}}

v_xD = \sqrt {V_0 ² + 4V_0 ²\sin² \alpha}

v_xD = \sqrt {V_0 ² (1+ 4\sin² \alpha)}

et donc après v_xD = V_0 (1 + 2\sin\alpha)}

Posté par
vanoisere : Mouvement parabolique d'une balle 07-10-21 à 16:55

Erreur déjà signalée :
Cours de math :

\sqrt{a^{2}+b^{2}}\neq a+b

Posté par
tintin22re : Mouvement parabolique d'une balle 07-10-21 à 17:02

Euh oui excusez moi...
Mais comment dois je simplifier la racine carré ?

Posté par
tintin22re : Mouvement parabolique d'une balle 07-10-21 à 17:18

Mis à part v_xD = (V_0²(1 + 4\sin²\alpha))-1/2

Posté par
vanoisere : Mouvement parabolique d'une balle 07-10-21 à 19:46

Puisque t_{B}=\frac{V_{o}.\sin\left(\alpha\right)}{g} :

v_{yD}=-2g.t_{B}+V_{o}.\sin\left(\alpha\right)=-V_{o}.\sin\left(\alpha\right)=-v_{yO}

De plus : v_{xD}=v_{xO}=V_{o}.\cos\left(\alpha\right)

Puisque : \cos^{2}\left(\alpha\right)+\sin^{2}\left(\alpha\right)=1, on obtient simplement :

v_{D}=V_{o}

On peut maintenant réfléchir au réalisme du résultat. En absence de frottement, l'énergie mécanique se conserve. Puisque les points O et D sont à la même altitude, l'énergie potentielle est la même en ces deux points, donc l'énergie cinétique est aussi la même en O et D.

On peut aussi remarquer que la trajectoire parabolique présente comme axe de symétrie la verticale passant par B. Les points O et D étant symétriques par rapport à cet axe, il est logique que les composantes suivant x de la vitesse soient égales et les composantes suivant y opposées.

Posté par
tintin22re : Mouvement parabolique d'une balle 07-10-21 à 20:21

Merci beaucoup au final je n'ai pas simplifier au maximum mon v_yD.
J'ai réfléchi a la question 7 mais  je n'ai trouvé aucune piste, auriez vous un indice ou un conseil pour me mettre sur la voix s'il vous plaît?

Posté par
vanoisere : Mouvement parabolique d'une balle 07-10-21 à 21:48

La portée est tout simplement xD.C'est la valeur de x si t=tD. Tu peux aussi exploiter la symétrie de la parabole dont j'ai précédemment parlé puisque tu connais déjà xB.

Posté par
tintin22re : Mouvement parabolique d'une balle 07-10-21 à 23:12

Je sais que la portée est xD mais dans cette question on me demande la portée maximum selon l'angle alpha et c'est a cause de cela que je ne vois pas comment faire...

Posté par
vanoisere : Mouvement parabolique d'une balle 08-10-21 à 14:32

Quelle expression obtiens-tu pour la portée ? Cette expression fait intervenir un sinus : quelle est la valeur maximale que peut prendre un sinus ? A quel angle correspond cette valeur maximale du sinus ?

Posté par
tintin22re : Mouvement parabolique d'une balle 11-10-21 à 19:29

Bonsoir excusez moi de ne pas vous avoir répondu plutôt je n'avais pas d'internet depuis vendredi....
Sinon la portée a pour équation x(t_D) = V_0 \cos (\alpha)t_D
x(t_D) =2V_0 \cos (\alpha) \frac {V_0 \sin(\alpha)}{g}

Soit x(t_D) = \frac {2V_0 ²}{g} + \frac {\cos(\alpha)\sin(\alpha)}{g}

On isole le cosinus et le sinus car l'angle varie avec, la première fraction est simplement une constante.
Donc on cherche l'angle avec la portée maximale de (cosinus * sinus) / g Donc \cos(\alpha)\sin(\alpha)g-1
On dérive puis on fait le tableau de variation pour trouver la valeur maximale ? C'est ce que vous me disiez , non?

Posté par
vanoisere : Mouvement parabolique d'une balle 11-10-21 à 20:12

Cours de math :
2cos().sin()=sin(2)

Posté par
tintin22re : Mouvement parabolique d'une balle 11-10-21 à 21:01

Donc x(t_D) = \frac {V_0 ² \sin(2\alpha)}{g}

La valeur max d'un sinus dans cet exo est pi/2 or la portée serait nulle donc je ne vois pas comment trouver la valeur de l'angle

Posté par
vanoisere : Mouvement parabolique d'une balle 12-10-21 à 00:22

La portée maximale correspond à un sinus égal à 1 :
2=/2
=/4 (en radian)
En athlétisme, on apprend que pour lancer un corps le plus loin possible (lancer du "poids" par exemple), le "poids" doit quitter la main du lanceur avec une inclinaison d'environ 45°. La situation est un peu plus complexe que dans cet exercice  à cause des frottements de l'air qui ne sont pas pris en compte ici.

Posté par
tintin22re : Mouvement parabolique d'une balle 12-10-21 à 08:53

D'accord je me compliquait bien la vie encore.... Je vous remercie j'avais la bonne réponse mais pas la démarche . Je vous remercie pour toute l'aide que vous m'avez apporté pour cet exercice.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !