Bonjour
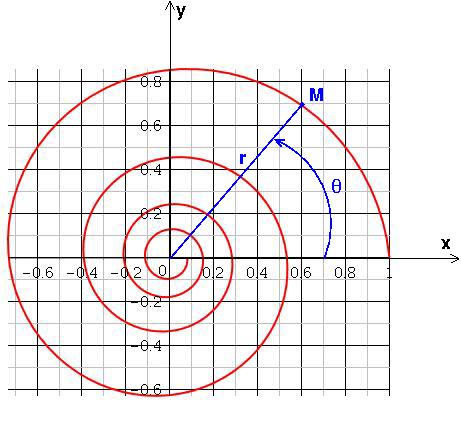
Le point M tourne à vitesse angulaire constante tout en se rapprochant du point O. La trajectoire est une spirale exponentielle.

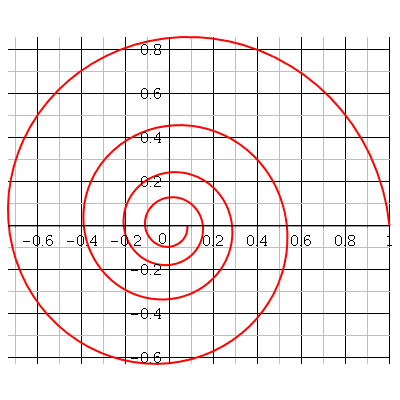
Pour illustrer mon message précédent, voici la trajectoire dans le cas particulier :
b=1 ; to=10 ; =1. (unités non précisées que je considère comme arbitraires). J'ai réalisé le tracé sur quatre tours.
A t=0, le point M occupe la position (r=1, =0) Il tourne ensuite dans le sens trigonométrique tout en se rapprochant de l'origine O du repère.

commente avez vous trouvé les valeurs de b w et to ?

J'ai choisi des valeurs totalement au hasard, juste pour te montrer l'allure de la trajectoire.

ah , et je peux utiliser les valeurs que je veux , ou bien il faut que je fasse le calcul ?

Tu ne fournis pas l'énoncé complet de l'exercice. Je ne peux pas me montrer catégorique. Cependant, si l'énoncé commence comme tu l'as indiqué, mon explication  du message de 18h54 peut suffire si tu l'accompagnes d'un tracé de spirale à main levée. L'énoncé parle "d'allure" de la trajectoire, pas de tracé précis.

non , c'est l'énoncé complète , j'ai juste deux questions quels sont les deux axes que tu as pris , et quels valeurs avez vous donné à teta merciii !!

Le schéma ci-dessous que j'ai complété va répondre à une partie de tes questions. Sinon, j'ai effectué un tracé sur 4 tours soit de =0 à =8 rad

ahh j'ai compris merciii beaucoup monsieur