Inscription / Connexion Nouveau Sujet
mouvement d'un projectile dans plan vertical
bonjour,j'ai eu des problèmes à traiter cet exercice qui faisait partir des exercices de notre sujet de composition de mécanique des points. j'ai cependant utilisé la relation fondamentale de la dynamique mais vers la fin je bloque.....aidez moi
un projectile ponctuel M de masse m est lancé d'un point O avec une vitesse initiale v(0) contenue dans le plan vertical Oxy et faisant l'angle α avec l'axe horizontal Ox. il est soumis à une force de freinage proportionnelle à sa vitesse:F=-kV, ou k est une constante positive.
1- Écrire les équations différentielles du mouvement.
2- En déduire les composantes Vx et Vy de la vitesse. Que deviennent-elles lorsque t tend vers l'infini ?
3-Calculer l'impulsion des forces appliquées entre les instants zéro et t. Que deviennent ses composantes lorsque t tend vers l'infini? En déduire les composantes de la vitesse limite.
Salut,
* le système est le projectile de masse m et de centre d'inertie M.
* le référentiel est le sol, terrestre supposé galiléen
* Bilan des forces :
- le poids de la basse
- la force de freinage
* Schéma (force de frainage à ajouter)
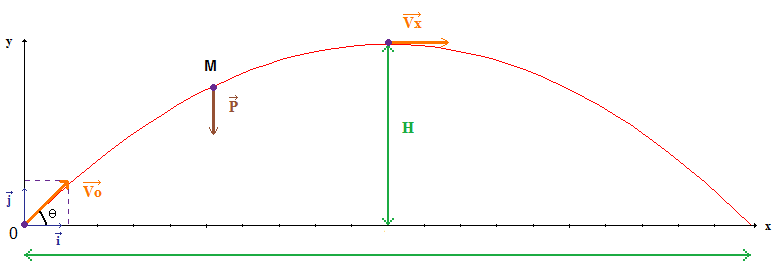
* D'après le principe fondamental de la dynamique,
<=>
on projette cette relation par rapport à x et y pour avoir les composantes vx et vy puis x(t) et y(t)


