Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... AutreForum autre de supérieur PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau autre
Partager :

mouvement d'un électron dans un champ électrique uniforme

Posté par
ptitesheena 20-02-10 à 20:15

Bonjour je suis coincé sur l'exercice le plus difficile de ma vie et j'ai beaucoup de question.

On s'intéresse au mouvement d'un électron de masse m et de charge électrique  -e < 0 dans un champ électrique E=-E0ey avec E0> 0 entre deux armature métalliques. (le poids de l'électron est négligeable dans le problème).

L'électron entre dans la zon ou le champ est non nul a un instant t=0 en O a une vitesse 0=V0ex où v0>0. Puis lélectron entre dans une zone où le champ électrique est nul.


Pour commencer je n'arrive pas as trouver les équations différentielles de x et y, mais je sais que je dois faire le bilan des forces et ensuite appliqué le principe fondamental de la dynamique.

Puis dans la question suivante on me demande de déterminer x(t) , y(t) et z(t) mais n'es pas la même chose que de donner les équations différentielles de x , y et z ?

Merci d'avance.

mouvement d\'un électron dans un champ électrique uniforme

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !     

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 20-02-10 à 22:03

Bonsoir,
Si c'est l'exercice le plus difficile de ta vie, qu'est-ce que ça va être les autres ?...
Quelle est la force qui s'exerce sur l'électron (il n'y en a qu'une puisqu'on néglige le poids) ?

Posté par
ptitesheenare : mouvement d'un électron dans un champ électrique uniforme 20-02-10 à 22:07

en faite je prefere pas penser au exercices futurs
euh je pense que la force c'est la force electrostatique

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 20-02-10 à 22:15

Oui, à quoi est-elle égale ?

Posté par
ptitesheenare : mouvement d'un électron dans un champ électrique uniforme 20-02-10 à 22:25

donc elle est égale a -Eo*ey
normalement -Eo*ey=ma
donc a=(-Eo*ey)/m
et es que l'on doit intégrer aprés

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 20-02-10 à 22:39

T'en as perdu en route... Il y a la charge qui intervient...
La force électrostatique est \vec{F}\,=\,q\,\vec{E}.
Ici, on a donc : \vec{F}\,=\,(-e)\,(-E_0)\,\vec{e_y}\,=\,e\,E_0\,\vec{e_y}
Donc :
3$a_x\,=\,\frac{d^2x}{dt^2}\,=\,0

3$a_y\,=\,\frac{d^2y}{dt^2}\,=\,e\,E_0

3$a_z\,=\,\frac{d^2z}{dt^2}\,=\,0

Posté par
ptitesheenare : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 16:20

euh j'ai pas tous compris .......

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 16:43

Il va falloir que tu me dises ce que tu n'as pas compris...
Je n'ai fait qu'appliquer la formule de la force électrostatique...
Et après je me suis trompé...
J'ai voulu appliquer la 2ème loi de Newton et j'ai réussi à me tromper, je suis allé un peu trop vite... Je ne me félicite pas !...
m\,\vec{a}\,=\,\sum\vec{F}
On a Fx = 0, Fy = eE0 , Fz = 0
Et on projette sur les axes.
Donc :
3$m\,a_x\,=\,m\,\frac{d^2x}{dt^2}\,=\,0

3$m\,a_y\,=\,m\,\frac{d^2y}{dt^2}\,=\,e\,E_0

3$m\,a_z\,=\,m\,\frac{d^2z}{dt^2}\,=\,0

Où cela bloque-t-il ?

D'autre part, tu es dans la catégorie "Autre" mais tu es dans quelle classe en fait ?
Tu es au moins en première année de fac ou en maths spé, vu l'exercice... A moins que ces notions soient vues dans certaines terminales...

Posté par
ptitesheenare : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 16:49

ah oui je comprend il sufisait d'appliquer le principe fondamental de la dynamique je vois je ne sais pas pourquoi je n'y est pas pensée.
Et je suis en premiére année de classe prépa donc je mets toujours mes sujets dans autres.

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 16:51


Donc :
3$a_x\,=\,0

3$a_y\,=\,\frac{e}{m}\,E_0

3$a_z\,=\,0

Tu ne connais pas l'écriture   3$\frac{d^2x}{dt^2}  ,  3$\frac{d^2y}{dt^2}  ,  3$\frac{d^2z}{dt^2}  ?

Citation :
je n'arrive pas as trouver les équations différentielles de x et y

On te demande explicitement les équations différentielles ?

Posté par
ptitesheenare : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 16:55

si je connais c'est écritures mais je ne l'ai comprend pas trés bien.
oui on me demande: "Trouver les équations différentielles vérifiées par les coordonées cartsienne x,y et z de l'électron" en toute lettre.

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 16:56

Citation :
Et je suis en premiére année de classe prépa donc je mets toujours mes sujets dans autres.

Il y a une catégorie "Supérieur" où il y a une sous-catégorie "Maths sup" (et non pas Maths spé comme j'ai écrit précédemment).

Dans la région où règne le champ électrique, quand on exprime y en fonction de x (y = f(x)), on obtient une parabole (après avoir éliminé t).

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 17:07

Citation :
je connais cette écriture mais je ne la comprends pas trés bien

Il n'y a pas grand-chose à comprendre. Ce n'est qu'une notation, une façon d'écrire...
La dérivée première s'écrit  3$\frac{dx}{dt}  . C'est la même chose que x' ...
La dérivée seconde s'écrit   3$\frac{d^2x}{dt^2}  . C'est la même chose que x" ...
Et ainsi de suite...

Si on te demande les équations différentielles, il faut écrire :
3$\frac{d^2x}{dt^2}\,=\,0  ou, à la limite :  3$x''\,=\,0

3$\frac{d^2y}{dt^2}\,=\,\frac{e}{m}\,E_0  ou, à la limite :  3$y''\,=\,\frac{e}{m}\,E_0

3$\frac{d^2z}{dt^2}\,=\,0  ou, à la limite :  3$z''\,=\,0

Et après, il faut intégrer en x, y et z.
(en intégrant  3$\frac{d^2x}{dt^2}  , on obtient  3$\frac{dx}{dt} , etc..., sans oublier les constantes d'intégration).

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 17:11

Si tu ne sais pas le faire, je te montre comment on fait évidemment mais il faut que tu aies compris comment on arrive aux équations différentielles du message précédent...

Posté par
ptitesheenare : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 17:14

Oui j'ai bien compris comment on en arrive aux equations différentielles.
merci ce fut très instructif ^^.

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 17:19

Si tu as d'autres blocages ...

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 21-02-10 à 17:20

Tu peux aussi mettre tes solutions si tu veux une vérification...

Posté par
poulicoure : mouvement d'un électron dans un champ électrique uniforme 01-11-10 à 15:23

Bonjour, je suis moi aussi en maths sup, et j'ai eu le même exercice, mais je n'arrive pas à faire certaines questions. On me demande tout d'abord de donner l'expression de l'énergie cinétique de l'électron en fonction de e, m, v0, E0 et x.
J'arrive à d(Ec)/dt = (e²*E0²)/m
Or, je sais que d(Ec)/dt devrait étre égal à la force électrostatique..
Pourriez vous m'aider s'il vous plait ?

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 01-11-10 à 18:18

Bonjour,
Je te propose :

3$m\,a_x\,=\,m\,\frac{d^2x}{dt^2}\,=\,0

3$m\,a_y\,=\,m\,\frac{d^2y}{dt^2}\,=\,e\,E_0

3$m\,a_z\,=\,m\,\frac{d^2z}{dt^2}\,=\,0

D'où :
3$\frac{dx}{dt}\,=\,v_0

3$\frac{dy}{dt}\,=\,\frac{e\,E_0}{m}\,t      (v_{y0}\,=\,0)

3$\frac{dz}{dt}\,=\,0

D'où :
3$x\,=\,v_0\,t

3$y\,=\,\frac{e\,E_0}{2m}\,t^2  

3$\frac{dz}{dt}\,=\,0

On a :
3$E_c\,=\,\frac{1}{2}mv^2\,=\,\frac{1}{2}m(v_x^2+v_y^2)\,=\,\frac{1}{2}m\,\big(v_0^2+\big(\frac{e\,E_0}{m}\big)^2\,t^2\big)
3$x\,=\,v_0\,t\,\Rightarrow\,t\,=\,\frac{x}{v_0}
3$E_c\,=\,\frac{1}{2}m\,\big(v_0^2+\big(\frac{e\,E_0}{m}\big)^2\,(\frac{x}{v_0})^2\big)
3$E_c\,=\,\frac{1}{2}\,m\,\big(v_0^2+\big(\frac{e\,E_0}{m\,v_0}\big)^2\,x^2\big)

Cela doit répondre à la question...

Posté par
poulicoure : mouvement d'un électron dans un champ électrique uniforme 02-11-10 à 10:56

Oui la réponse est bonne mais on nous demande dans un premier temps de trouver ce résultat par application du théorème de l'énergie cinétique ... il y a deux énoncés dEc/dt=somme des puissances des forces ; et il y a l'expression avec 1/2mv^2(au point lambda) - 1/2mv^2(a un autre point omega) . Il faut utiliser la première expression puisqu'on a pas les vitesse pour la deuxième expression? Merci .

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 02-11-10 à 14:09

Bon...OK
3$\frac{dE_c}{dt}\,=\,\sum\,\vec{F}\,.\,\vec{v}
3$\vec{F}\,.\,\vec{v}\,=\,F_yv_y\,=\,eE_0\frac{eE_0}{m}t
3$\frac{dE_c}{dt}\,=\,\frac{(eE_0)^2}{m}t
3$E_c\,=\,\frac{(eE_0)^2}{2m}t^2\,+\,E_{c0}
A t = 0, E_{c0}\,=\,\frac{1}{2}mv_0^2
D'où :
3$E_c\,=\,\frac{(eE_0)^2}{2m}t^2\,+\,\frac{1}{2}mv_0^2
3$x\,=\,v_0\,t\,\Rightarrow\,t\,=\,\frac{x}{v_0}
3$E_c\,=\,\frac{(eE_0)^2}{2m}\big(\frac{x}{v_0}\big)^2\,+\,\frac{1}{2}mv_0^2
Que l'on peut écrire :
3$E_c\,=\,\frac{1}{2}m\,\Big(\big(\frac{eE_0}{mv_0}\big)^2x^2\,+\,v_0^2\Big)

Posté par
nan0u001re : mouvement d'un électron dans un champ électrique uniforme 05-11-10 à 17:07

Bonsoir, J'ai un exercice un peu similaire.
Il s'agit de trouver les équations différencielles qui régit le mouvement de l'électron sauf que dans l'exo il y a la force électromagnétique et une force de frottement.
Comment j'écris l'équation différencielle suivant Oz?
merci d'avance pr les éventuelles réponses
bonne soirée

Posté par
Marc35re : mouvement d'un électron dans un champ électrique uniforme 05-11-10 à 21:11

Bonsoir,
Précise un peu ton exercice...
Le mieux serait de mettre le texte en entier.
Est-ce une force électrique seulement ou un champ magnétique ou les deux? Selon quels axes ?
etc...

Posté par
Lauriianesuite mouvement d'un électron dans champ uniforme 03-03-14 à 15:22

Bonjour,
je suis étudiante en BCPST1 et j'ai moi aussi ce même sujet en devoir.
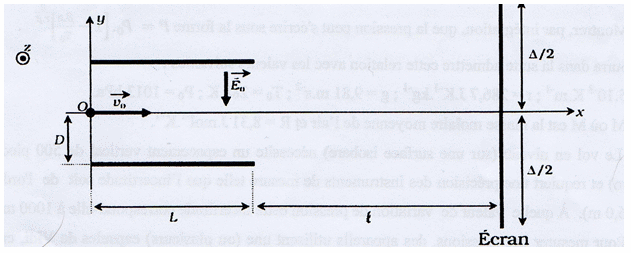
Après l'étude du mouvement et l'étude énergétique il y a d'autres questions concernant la déviation de l'électron vers l'écran. ( Après être passé dans l'armature, l'électron sort de cette zone pour x=L et finit sa course sur un écran situé en x=L+l où son impact active un pixel. La taille de l'écran dans la direction (Oy) est notée ).

La première question demande d'exprimer le vecteur vitesse dans la base cartésienne, en fonction de e,m,L,Vo et Eo avec lequel l'électron quitte la zone entre les armatures.

je pensais partir de x=L.
puis j'ai pensé utiliser l'expression de y en fonction de x,
mais cela ne dois pas être ça, car on obtient des constantes, ce qui donne Vx et Vy nuls...

Si vous pouviez me donnez un petit indice.
Merci d'avance.
Bonne continuation.


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !