Inscription / Connexion Nouveau Sujet
mouvement d'un cerceau
salut ,
merci de me donner des indices pour la question 2 et 3
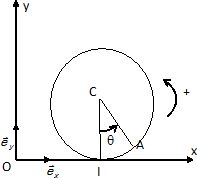
Un cerceau homogène de masse m, de centre C et de rayon a roule sans glisser sur l'axe Ox d'un repère galiléen. Le cerceau est astreint à se déplacer dans le plan vertical yOx.
On désigne par I le point de contact du cerceau avec le sol, par A un point fixe du cerceau, par x l'abscisse instantanée de C. A l'instant t=0, x=0 et =0.
1/ La relation entre x et q est : x = a.
2/ En utilisant le théorème de Koenig, déterminer l'énergie cinétique du cerceau dans le repère R en fonction de m et x.
3/ déterminer l'expression de la vitesse vA du point A dans R, exprimée dans le repère xOy.
Bonjour handa,
Pourrais-tu rappeler le fameux théorème de Koenig ? Qu'est-ce qui est bloquant le connaissant ?

Je sais que l'énergie cinétique d'un solide dans un référentiel est :
Ec=Ec(G/R)+Ec(S/RG)
RG : référentiel barycentrique
Mais je ne comprend rien à propos de cette relation.
Oui, merci pour le lien c'est exactement ce que je cherche.
Mes questions sont les suivantes :
* on a un seul corps donc l'énergie cinétique est 1/2mv2
Pourquoi donc on applique ce théorème ?
* pourquoi en ajoute 1/2.J.w2??
*Lorsqu'il faut chercher l'énergie cinétique de ce cerceau sans le lest, on applique le théorème de Koenig, jusqu'ici je comprends. Mais lorsqu'on nous demande de chercher l'énergie cinétique du cerceau lesté, on calcule simplement (1/2)mVa². Je ne comprends pas donc pourquoi on n'appliquer pas le théorème de Koenig dans les 2 cas.
Merci d'avance
Il ne faut pas oublier qu'il y a deux mouvements dans l'affaire : le cerceau tourne sur lui même et il se déplace linéairement sur le sol.
Tu as très certainement vu l'énergie cinétique d'un solide en rotation entour d'un axe (ici (Gz)) : Ec = 1/2.J.w².
Ensuite l'énergie cinétique sous sa forme générale est Ec' = 1/2.m.v².
Enfin, si le cerceau roule sans glisser, tu peux relier v et w par une relation ...