Inscription / Connexion Nouveau Sujet
Mouvement cycloïdal : transformation Galilée
Bonjour, je suis en première année de licence mathématiques mais j'ai tout de même quelques cours de physique. J'ai un exercice à résoudre mais je suis bloquée car certaines notions n'ont pas été abordées en cours et je ne comprends pas l'exercice. Voici l'énoncé :
Transformation de Galilée : mouvement cycloïdal
Un disque D de rayon R roule sans glisser sur l'axe Oy d'un référentiel R (O; x, y, z).
Le centre O' du disque, auquel on associe le référentiel R'(O; x' ,y', z') dont les axes sont
parallèles à ceux de R, est animé d'un mouvement rectiligne uniforme, de vitesse v0 parallèle à Oy. Soit M un point situé sur la circonférence du disque et I le point de contact du disque avec l'axe Oy. A l'instant t = 0, M est confondu avec O.
1. Etablir, à l'instant t, l'expression des vecteurs position OM et O'M en fonction de v0 et de R dans la base B (ex, ey, ez). En déduire la nature de la trajectoire (T) décrite par M
dans R :
(a) Déterminer et représenter sur une figure :
• les vecteurs vR'(M), v e (R'/R) et en déduire la vitesse du point M dans R.
• les vecteurs aR'(M), ae (R'/R) et ac
(b) Comparer les accélérations du point M dans R et R'
Conclure.
(c) Calculer la longueur curviligne s parcourue par M lorsqu'il rencontre l'axe Oy pour la première fois.
(d) Quel est l'angle entre le vecteur IM et le vecteur unitaire et tangent en M à la trajectoire (T) ?
(e) Trouver à l'instant t :
• une relation entre la composante normale de l'accélération du point M : aRn(M) et la longueur IM
• la position du centre de courbure C de la trajectoire (T).
Merci pour votre aide 
Bonsoir
Le plus simple, pour une aide efficace, serait que tu scannes ton schéma complété avec les différents vecteurs utiles, pour le poster ici. Ensuite, explique ce que tu as réussi à faire et pose des questions précises sur ce qui te bloque.
Bonsoir,
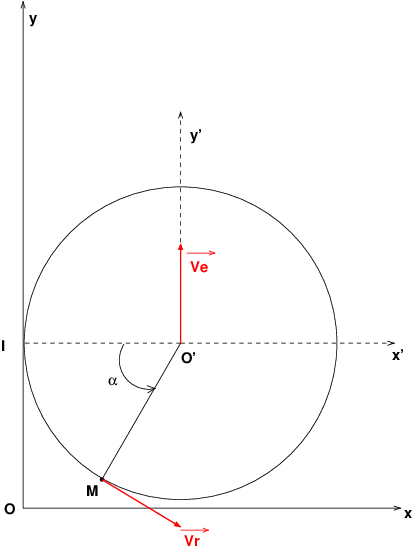
Voici le schéma que j'ai réalisé, j'espère qu'il est assez lisible. J'ai représenté en vert le vecteur v0 qui, si je ne me trompe pas, est égal au vecteur ve(R'/R). En noir il s'agit du vecteur unitaire et tangent à la trajectoire T au point M. Ce début de schéma est-il juste?
Voici les différentes questions que je me pose :
1- par quels moyens puis-je trouver l'expression des vecteurs OM et O'M?
2-La trajectoire T est-elle cycloïdale?
3-Comment puis-je représenter le vecteur vR'(M) et les différents vecteurs accélérations ?
4-La longueur curviligne s parcourue par M entre t=0 et le moment où M rencontre l'axe Oy est-elle de 2*
*R ?
5-Comment retrouver la valeur de l'angle entre IM et et (j'ai pensé qu'il s'agissait d'un angle droit mais je ne suis pas certaine) ?
6-Que signifie "composante normale de l'accélération" ?
7-Qu'est-ce qu'un "centre de courbure" ?
J'espère que mes questions sont assez claires. Merci pour vos retours !
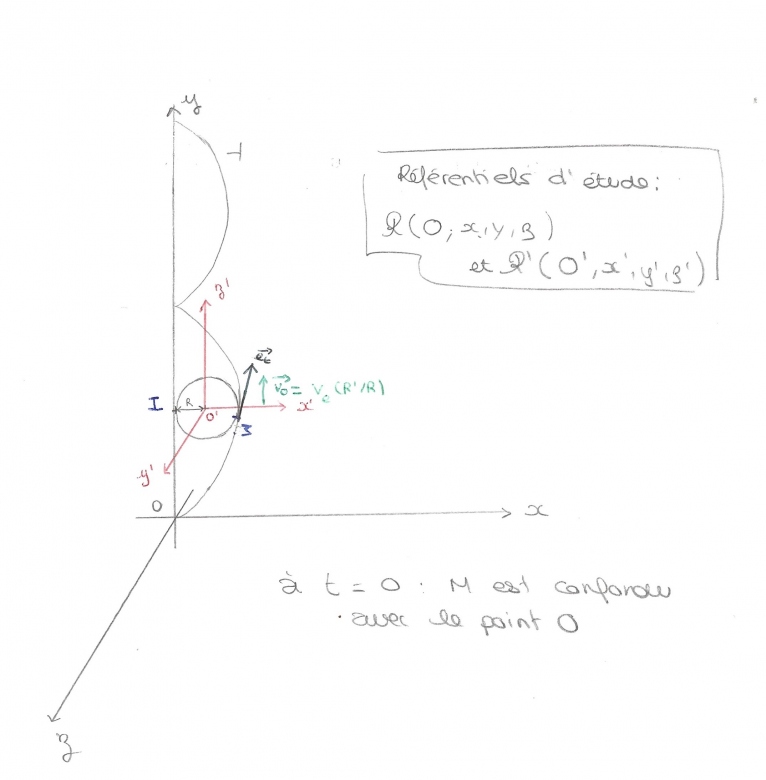
Tu peux te contenter de travailler en 2D puisque le mouvement est plan. Pas le temps ce soir de te faire un schéma plus propre. Tu aurais sans doute intérêt à choisir le point I plus près du point O de façon à ce que l'angle de rotation depuis l'instant initial soit inférieur à pi/2 (60° environ par exemple). Il est intéressant alors de remarquer que, comme le disque roule sans glisser, la distance OI est aussi égale à l'arc IM aussi égal à R.
où est l'angle de rotation depuis l'instant initial.
Pour ne pas te tromper par la suite : plus simple de choisir O'X' parallèle à OX et O'Y' parallèle à OY.
Bonjour,
Merci beaucoup pour ce schéma plus clair et plus complet!
Puisque OI = IM = R alors OM = 2R ? v0 n'intervient donc pas dans l'expression de OM?
Sur votre schéma l'angle 
correspond-il à l'angle dont vous avez parlé ?
Merci.
Non. Tu obtiens les coordonnées de M en écrivant :
Les coordonnées de M dépendent des coordonnées de P'tit, de R et de (voir figure ).
Le plus difficile à comprendre réside dans l'égalité entre y(O')=OI et la longueur du l'arc IM. Tu peux éventuellement faire l'expérience consistant à faire rouler sans glisser un disque sur une table.
Annuler
connectez vous