Inscription / Connexion Nouveau Sujet
Mouvement Cycloïdal
Bonjour, j'ai besoin de votre aide svp pour résoudre cet exercice; [u][/u]énoncé : une roue circulaire de centre c, et de rayon R,roule sans glisser sur l'axe OX' tout en restant dans le plan (O,X,Z),un point A de la roue coïncide à l'instant t=0 avec l'origine O avec (Vc=cte) , déterminer les coordonnées de point A à l'instant t??? [rouge][/rouge]
Bonjour, j'ai besoin de votre aide svp pour résoudre cet exercice; [u][/u]énoncé : une roue circulaire de centre c, et de rayon R,roule sans glisser sur l'axe OX' tout en restant dans le plan (O,X,Z),un point A de la roue coïncide à l'instant t=0 avec l'origine O avec (Vc=cte) , déterminer les coordonnées de point A à l'instant t??? [rouge][/rouge]

Bonjour
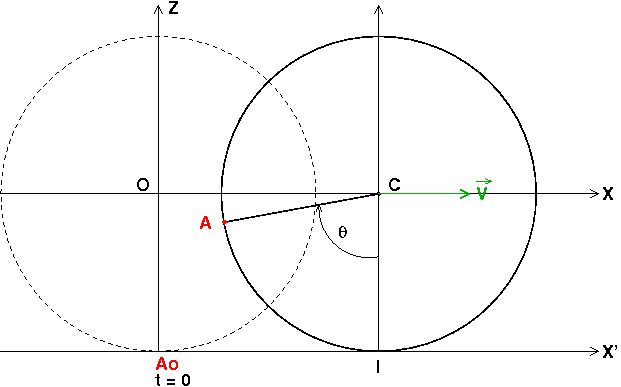
Commence par faire un schéma et note , par exemple,  , l'angle de rotation de la roue à partir de l'instant initial.
, l'angle de rotation de la roue à partir de l'instant initial.
Les coordonnées cartésiennes de A s'expriment alors simplement en fonction de xC, R et  . Le fait que la roue roule sans glisser va te fournir une relation simple entre xC et
. Le fait que la roue roule sans glisser va te fournir une relation simple entre xC et  . La suite est facile.
. La suite est facile.
Je te laisse réfléchir à tout cela et proposer une solution. Si tu n'y arrives pas, redemande de l'aide...
Merci beaucoup Vanoise, j'ai trouvé X=R(ø-sinø)
Y=R(1-cosø)
Ce sont des equations connus du mouvement Cycloïdal mais comment peut-on les tirer d'après le schéma je sais pas ?
À la date t = 0, le centre C est en O, le point A est en Ao. À la date t quelconque, les coordonnées du centre C sont :
Les coordonnées du point A à la date t quelconque sont :
Condition de roulement sans glissement. Plusieurs méthodes sont possibles. La plus directe consiste à remarquer que la distance OC = V.t est aussi égale à la longueur de l'arc IA :
On peut aussi écrire que la vitesse du point I de contact avec le plan horizontal est le vecteur nul. Cela conduit à :
Par intégration puisque V est une constante : . Puisque
pour t = 0, la constante d'intégration est nulle. On obtient bien le même résultat. Au final :
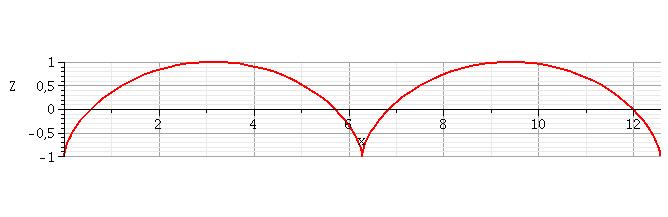
Voici la trajectoire obtenue après deux tours effectués pour R = 1m.