Inscription / Connexion Nouveau Sujet
Mouvement circulaire d'une roue
Bonjour à tous !
Voici le sujet d'un exercice :
Une roue de rayon R roule sans glisser sur un axe horizontal Ox. Le mouvement de la roue est donné par l'angle 
que fait le rayon de la roue avec la position initial à t=0
Questions :
1) Quelles sont les coordonnées cartésiennes x(t) et y(t) du point M ?
2) Déterminer les composantes des vecteurs vitesse et accélération du point M en fonction de R et de .
3) Donner les valeurs du vecteur vitesse/accélération au moment ou M retouche le sol.
4) On suppose maintenant que le mouvement du centre de la roue est rectiligne uniforme à la vitesse v0.
Montrer que l'accélération est centripète vers O et chercher son module en fonction de v0 et R.
Voila ce que je propose :
1) x(t)=R
sin() et y(t)=-Rcos()
2) Je dérive simplement mes expressions
3) J'évalue mes expressions en 
0[2
)
4) Voila ou est mon soucis : je ne vois pas du tout comment utiliser v0. Je pense qu'il faudrait chercher à exprimer le vecteur position au point M puis dérivé deux fois, afin de trouver une expression de l'accélération sous la forme a=an+at ou an=-R' 2et at=R'' et comme on a une vitesse constante, on aurait ' = cste donc ''=0 d'ou a=an et alors l'accélération est bien centripète ! Le problème est que je n'arrive pas à utiliser ce v0 ...
Merci d'avance pour votre aide !!
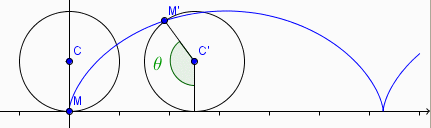
bonjour,
1) OM = OA + AC + CM (cf dessin) (vecteurs en gras)
OA = R
(je te laisse le démontrer)
AC = R
CM = ...
donc
x(t) = R + ...
y(t) = R + ...
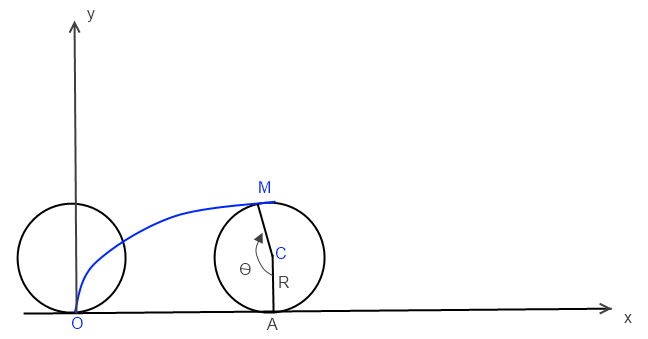
Bonjour, j'ai repris le dessin sur un forum, et c'est peut être pour ça que c'est pas très clair :
Sur le dessin C = O dont je parle dans les questions, c'est l'origine mobile du repère...
tu appelles les points comme tu veux, ça ne change rien au raisonnement
(c'est pour cela que je mets toujours un dessin en annexe)
Encore une fois désolé si ce n'est pas claire, mais l'origine du repère n'est pas celle que tu as placé. C'est une origine mobile qui correspond au centre du cercle, à tout instant t.
d'accord, je commence à saisir...
(de l'intérêt de poster un dessin en rapport avec le texte 
1) x = -R sinO (cf nouveau dessin)
y = -R cosO
2) tu as calculé 
M, l'accélération absolue de M
4) si le mvt d'entrainement est une translation uniforme, on a
RO' = vo
et O" = 0
donc M ça doit se simplifier nettement
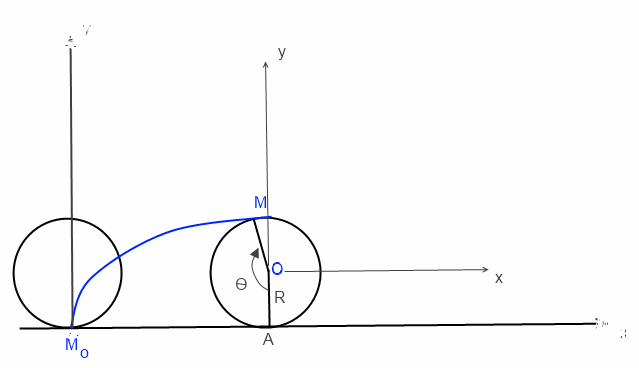
Merci pour ta réponse !
Je comprends pas tellement le R'=v0 pourrait tu le justifier stp?
Aussi, je peux trouver un signe différent pour y(t) si j'oriente dans le sens trigo non?
(A) = 0 donc vo - RO' = 0
Annuler
connectez vous