Inscription / Connexion Nouveau Sujet
Mouvement Central exo1
Bonjour, je voudrai de l'aide pour mon exercice que voici
Exercice:
La trajectoire d'un point matériel est animé d'un mouvement central,l'origine du repère O étant le centre des accélerations,est donnée par l'hyperbole d'équation :
xy=k avec k une constante positive.
Sans calculer x(t) et y(t) montrer que le vecteur accéleration est le rayon vecteur sont colinéraires et de même sens
Ce que j'ai fait:
Notons r(point)=r' et theta(point)=theta prime
Bon comme c'est un mouvement central alors l'acceleration est radiale alors le rayon vecteur et ar sont colinéaires d'où ont la même direction, maintenant je dois montrer que r"-r 2 et r ont même signe et le tour est joué
2 et r ont même signe et le tour est joué
Merci
Hello
Pourrais tu envisager de reformuler l'énoncé de ton exercice? il est qlq peu "exotique" (ex: mouvement central)
BonjourMolotov79 et bonjour dirac (bon retour !  )
)
Pourrais tu envisager de reformuler l'énoncé de ton exercice?
Ce serait effectivement une bonne idée car, tel que je comprends l'énoncé, et manifestement tel que Molotov79 l'a compris, il s'agirait de démontrer qu'en tout point, le vecteur accélération et le vecteur position
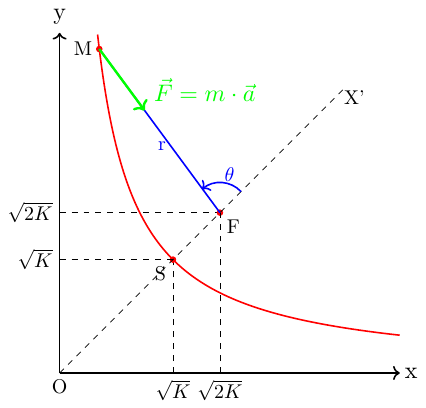
À mon avis, Inutile de perdre son temps à essayer de démontrer cela car l'hypothèse est fausse. L'équation cartésienne fournie correspond à une hyperbole équilatère qui est bien une trajectoire possible pour un mouvement à force centrale mais le centre de poussée n'est pas l'origine du repère mais le foyer F, point situé sur la première diagonale :
Il faudrait donc reformuler la question en demandant de démontrer que le vecteur accélération et le vecteur
Post-scriptum à mon message précédent : l'expression "centre de poussée" n'est pas très heureuse dans ce contexte. Il serait préférable de dire que la trajectoire de M s'explique par une force centrale exercée sur M constamment orientée de M vers F.
Hello vanoise (toujours fidèle au poste, bravo!)
Lorsque Molotov79 aura corrigé l'énoncé, on devra peut être aussi devoir envisager le cas d'une force répulsive, où par exemple une charge est au point F, et une autre de même signe parcours "l'autre branche" de l'hyperbole.
(enfin cette remarque est surtout là pour t'adresser un petit bonjour!)
toujours fidèle au poste, bravo!
Aucun problème depuis que la source des polémiques stériles a été éliminée le 30 août 2018 !

on devra peut être aussi devoir envisager le cas d'une force répulsive
Bien sûr ! Pour l'instant puisqu'il s'agit d'étudier un mouvement sous l'action d'une force centrale, l'essentiel est d'envisager une accélération colinéaire au vecteur FM et non colinéaire au vecteur OM.