Niveau école ingénieur

Moment quadratique (2)

Posté par
CloudNine 18-03-18 à 15:15

Bonjour,
J'ai un exercice à faire mais je ne sais pas comment faire aux questions (a) et (c)

Exercice:
Moment quadratique (2)
Calculer les caractéristiques des sections suivantes:
(a) : centre d'inertie
On cherche $G(z_{G},y{G}) = ?$
Par symétrie par rapport à y: $z_{G} = 0$
Je ne sais pas comment faire la suite

(b) : moment quadratique par rapport à y et z
Surface composée $S=S_{1} + S_{2}$
$I_{zz}= I_{zz} (S_{1})+I_{zz}(S_{2}) = \frac{R^{4} \pi}{8}+\frac{R^{4}}{3}$
$I_{yy} = \frac{\pi R^{4}}{8}+ \frac{R^{4}}{12}$

(c) : moment quadratique par rapport à $y_{G}$ et $z_{G}$
On applique le théorème d'Huygens: $I_{z_{G}z_{G}}=I_{zz}-S.d^{2}$

Je ne vois pas comment déterminer la suite et la distance, doit-on aussi appliquer le thm d'Huygens pour $I_{y_{G}y_{G}$ ?

Merci d'avance pour vos aides et vos explications
Cordialement,

Posté par re : Moment quadratique (2) 18-03-18 à 16:08

Pour le centre d'inertie G :
La position du centre d'inertie G1 du demi disque est donné soit par calcul direct soit par le théorème de Guldin :

$y_{G1}=\frac{4R}{3\pi}$
Evidemment pour G2, centre d'inertie du carré :

$y_{G2}=-\frac{R}{2}$
Le centre d'inertie G est le barycentre :

$\left(S_{1}+S_{2}\right).y_{G}=S_{1}.y_{G1}+S_{2}.y_{G2}$
Pour les moments, le théorème de Huyguens est une bonne idée maintenant que tu connais la position de G.

Posté par re : Moment quadratique (2) 18-03-18 à 19:14

D'accord avec tes moments quadratiques. Maintenant que tu sais situer le point G, le théorème de Huygens devrait te permettre de terminer.

Posté par re : Moment quadratique (2) 18-03-18 à 20:27

Bonsoir vanoise
Merci pour votre réponse.
Nous n'avons pas étudier le théorème de Guldin ( ou pas encore). Quelle est la formule afin de calculer le centre d'inertie par la méthode du calcul direct ?
Et pourquoi le centre d'inertie d'inertie du carré est égale à $\frac{-R}{2}$
Merci,

Posté par re : Moment quadratique (2) 18-03-18 à 20:53

Tu as quelques exemples de calculs, dont celui qui t'intéresse, ici :

Pour le carré, tu peux raisonner sur les axes de symétrie.

Posté par re : Moment quadratique (2) 19-03-18 à 12:53

Bonjour
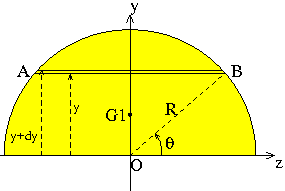
Le calcul direct proposé sur le site dont j'ai fourni la référence utilise la notion d'intégrale double ; voici une méthode alternative qu'il n'utilise pas d'intégrale double mais suppose un minimum de connaissances en trigonométrie...

On découpe le demi disque en bandes élémentaires (AB) parallèles à (O,y) d'aire élémentaire dS, situées à la distance y de l'axe (O,y). Par définition du centre d'inertie G1 de ce demi disque :

$y_{G1}=\frac{\iint y.dS}{S_{D}}$

Avec : $S_{D}=\frac{\pi.R^{2}}{2}$ : aire du demi disque.

$y=R.\sin\left(\theta\right)$

La longueur (AB) de la bande élémentaire vaut :
$\\ \left(AB\right)=2R.\cos\left(\theta\right)$

En dérivant par rapport à $\theta$ l'expression de y :

$\frac{dy}{d\theta}=R.\cos\left(\theta\right)$

La largeur élémentaire de la bande (AB) est ainsi :

$dy=R.\cos\left(\theta\right).d\theta$

L'aire élémentaire de la bande est ainsi :

$dS=2R^{2}.\cos^{2}\left(\theta\right).d\theta$

Ainsi :

$y_{G1}=\frac{\intop_{0}^{\frac{\pi}{2}}2R^{3}.\cos^{2}\left(\theta\right).\sin\left(\theta\right).d\theta}{\frac{\pi.R^{2}}{2}}=\frac{4R}{\pi}\cdot\intop_{0}^{\frac{\pi}{2}}\cos^{2}\left(\theta\right).\sin\left(\theta\right).d\theta$
$\\ y_{G1}=\frac{4R}{\pi}\cdot\left[-\frac{\cos^{3}\left(\theta\right)}{3}\right]_{0}^{\frac{\pi}{2}}=\frac{4R}{3\pi}$
À toi de voir laquelle des deux méthodes te convient le mieux.

Moment quadratique (2)