Inscription / Connexion Nouveau Sujet
Moment inertie
Bonjour,
Je n'arrive pas à calculer le moment d'inertie de ce cylindre.
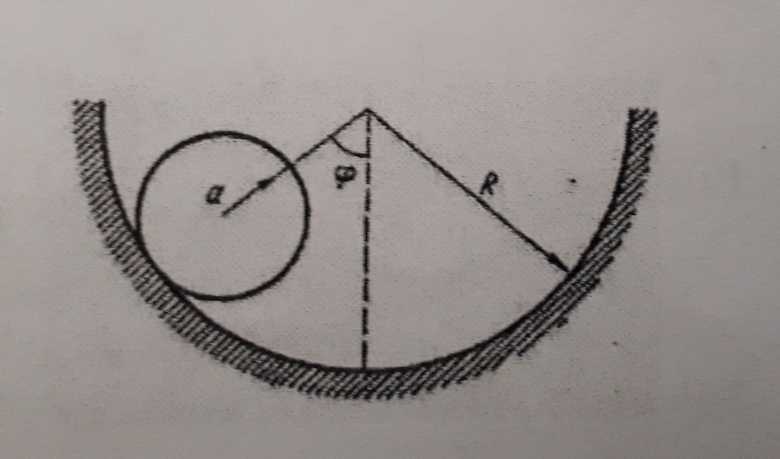
Énoncé: Trouver l'energie cinétique d'un cylindre homogène de masse m et de rayon a roulant à l'intérieur d'une surface cylindrique de rayon R.
Utilisons l'angle 
formé par la droite qui joint les centres des deux cylindres et la verticale.
La correction donne T=[3m(d/dt)2(R-a)2]/4
T=Ttranslation+Trotation
Tt=mV2/2
V=(R-a)(d/dt)
Tr=I(d/dt)2/2
I=Icm+Iao
I=(ma2/2)+(m(R-a)2)
Quelqu'un pourrait m'aider SVP ?
Bonjour
Il faut tenir compte de la condition de roulement sans glissement. Pour l'énergie cinétique, il ne s'agit pas de calculer un nouveau moment d'inertie mais plutôt d'appliquer le théorème de Koenig n° 3 sur l'énergie cinétique.
On a appris le théorème de transport/théorème de Huygens-Steiner. Je ne connais pas le théorème de Koenig.
Ou on dit I=mr2/2 avec r la distance distance du centre masse du cylindre au centre masse du système donc r=R-a ?
Dans le contexte de ce problème, le théorème de Koenig revient à écrire ce que tu as déjà compris : l'énergie cinétique est la somme de l'énergie de translation et de l'énergie de rotation mais tu n'a pas bien compris ce qu'est l'énergie de translation. La clé du problème réside dans la condition de roulement sans glissement. Il faut écire que les point du cylindre ont une vitesse nulle quand ils sont en contact avec la surface cylindrique fixe.
La condition de roulement sans glissement fournit une relation simple entre VG et ... Celle de ton corrigé.
Désolé : confusion de notation : La vitesse de rotation du cylindre autour de son axe n'est pas . On peut écrire :
La condition de roulement sans glissement fournit une relation simple entre VG et ... et comme VG s'exprime en fonction de
comme indiqué dans ton corrigé...
/dt)=v/a.
Annuler
connectez vous