Inscription / Connexion Nouveau Sujet
Moment en physique
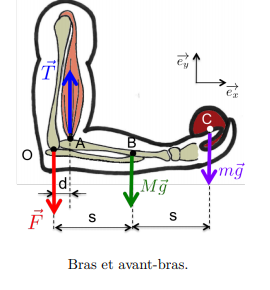
Un joueur de cricket tient une balle de masse m = 160 g dans sa main, son avant-bras de masse M = 1,2 kg étant horizontal. Le centre de masse de l'avant-bras est situé à une distance s = 17 cm du coude. La balle est à une distance 2s du coude.
Le tendon du biceps, attaché à une distance d = 2, 75 cm du coude, exerce une force T~, verticale orientée vers le haut et d'intensité 12,6 N, permettant de maintenir l'avant-bras horizontal. L'os du bras (humérus) exerce sur les os de l'avant-bras (radius et cubitus), au niveau de l'articulation du coude, une force F~ verticale orientée vers le bas (réaction du contact dans l'articulation).
Bras et avant-bras.
1. Calculer le moment résultant exercé sur l'avant bras, en utilisant le coude comme point de calcul (axe de rotation en O).
2. Si ce moment résultant n'est pas nul, dans quel sens tourne l'avant-bras autour du coude ?
3. Calculer la norme de T~ permettant d'annuler ce moment résultant.
Dans ce cas, quelle est l'intensité de la force F~ exercée par le haut du bras ?
Pour la première question est ce qu'il faut calculer le moment de cette façon
OO^(-F vecteur ey)+ OA^(T vecteur ey)+OB^(-mg vecteur ey) =0
Bonjour
La méthode de calcul est la méthode générale que tu peux appliquer ici mais tu as oublié le moment du poids de l'avant-bras.
Dans un problème aussi simple, on peut aussi utiliser la notion de "bras de levier". Utilise la méthode avec laquelle tu es le plus à l'aise.
OO^(-F vecteur ey)+ OA^(T vecteur ey)+OB^(-mg vecteur ey) + OC^(-mg vecteur ey) =0
y manquer cette partie là c'est ça ?
Voilà ce que je trouve
d vecteur ex ^(T vecteur ey) +s vecteur ex ^(-Mg vecteur ey) + 2s vecteur ex ^(-mg vecteur ey)
=> dT vecteur ez - Mgs vecteur ez - 2smg vecteur ez =0
en projection sur z :
dT-Mgs-2smg=0
2.75*10^-2*12.6-1.2*9.81*17*10^-2-2*17*10^-2*0.16*9.81
Mais quand je fais ce calcul je tombe sur un résultat négatif c'est normal ?
L'énoncé de la question 2 donne une indication...
Trois cas sont envisageables :
* Projection de la somme des moments suivant (Oz) nulle : équilibre ;
* Projection de la somme des moments suivant (Oz) positive : mouvement de rotation de l'avant bras dans le sens positif. L'axe (Oz) étant orienté vers l'avant de la figure. Le sens positif correspond au sens anti horaire : l'avant-bras tourne en montant.
* Projection de la somme des moments suivant (Oz) négative : mouvement de rotation dans le sens négatif soit ici le sens horaire (sens des aiguilles d'une montre). L'avant bras tourne en descendant. En clair : l'intensité de la force F n'est pas suffisante pour permettre de maintenir la boule en équilibre..
Ah d'accord merci , donc en faite la je suis dans le cas ou je tourne dans le sens horaire c'est pour cela que j'obtiens un résultat négatif si j'ai bien compris.
Pour la question 3 du coup, je dois résoudre
dT-Mgs-2smg=0 c'est bien ça ?
et extraire du coup T = Mgs+2smg/d
je trouve T=194N et pour calculer F je vois pas comment je dois faire
est ce que je dois utiliser vecteur de F + vecteur T = 0 ?
D'accord avec ton calcul de T. Pour obtenir F, il faut écrire que la résultantes de toutes les forces appliquées sur l'avant-bras est le vecteur nul. Ton calcul doit donc aussi tenir compte des deux poids.
vecteur de F + vecteur de T + vecteur de P1 + vecteur de P2= vecteur nul
=> F-T+Mg+mg =0
F=T-(Mg+mg)
F environ égale à 180 N



