Bonjour je vous poste tout d'abord le sujet sur le quel je travaille:

Le référentiel R0 est considéré comme galiléen ; il est rapporté au repère
(O₀, x₀ ,y₀, z₀) . Le
référentiel absolu R0 est associé au bâti (0).
On note R1 le référentiel rapporté au repère orthonormé direct
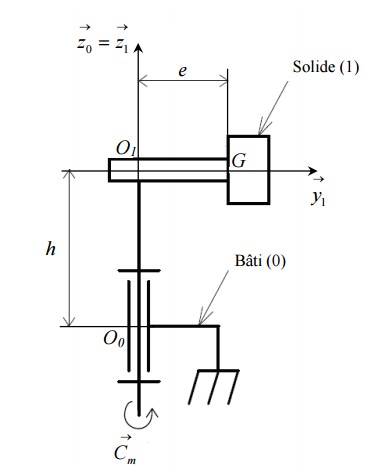
(O₁,x₁,y₁,z₁) tel que z₁=z₀.  Le repère R1 , lié rigidement au solide (1), se déduit à chaque instant de R0 par une rotation d'angle θ
autour de l'axe O₀ z₀ .
Un solide (1) de masse m et de centre de gravité G, défini par O₁G=ey₁ , est en liaison pivot d'axe
O₀z₀ , supposée parfaite, avec le bâti (0). Il est entraîné en rotation autour de l'axe O₀z₀ par
rapport au bâti (0) grâce à un couple moteur C_m=C_m z₀.

On note g= − g z₀ l'accélération de la pesanteur.
On donne O₀ O₁= h z₀ et O₁G=ey₁ .
La matrice d'inertie du solide (1) dans le repère ) (O₁,x₁,y₁,z₁) est : I₁(O₁)= .


1. Exprimer dans R1 la vitesse ) (V∈1/ 0) du point G appartenant au solide (1) par rapport
au bâti (0).
2. Exprimer dans R1 l'accélération ) Γ( G∈1/ 0) du point G appartenant au solide (1) par
rapport au bâti (0).
3. Exprimer dans R1 le moment cinétique L_O[sub]1[/sub](1/0) du solide (1) par rapport au bâti (0) au point O₁ .
4. Exprimer dans R1 le moment dynamique dL_0[sub]1[/sub](1/0) /dt du solide (1) par rapport au bâti (0)
au point O₁.
3.5 En déduire le couple moteur C_m=C_mz₀ nécessaire à la mise en rotation du solide (1) en
fonction de l'accélération angulaire θ'' .

A la question 4 j'ai calculé le moment dynamique avec deux méthodes mais j'obtiens deux résultats différents: la première avec le moment de O₁ par rapport à g l'accération de pesanteur me donne -emgx₁. La deuxième méthode en dérivant le moment cinétique me donne
Du coup j'obtiens comme couple moteur C_m=C''z₀.
J'aimerais savoir où est ma faute dans le calcul du moment des forces extérieures car j'ai simplement appliqué la formule du cours.

Merci d'avance.