Inscription / Connexion Nouveau Sujet
Moment d'1 champ magnétique sur circuit fermé
Bonjour,
Soit un circuit fermé rectangulaire, où un courant passe dans le sens horaire. Il y a un champ magnétique uniforme, dirigé vers la droite.
Soit un point situé au milieu de la branche gauche (verticale) du circuit. Ce point
est le point à partir duquel je veux calculer le moment total des forces de Lorentz.
Soit le vecteur unitaire allant de gauche à droite,
celui allant du bas vers le haut (dans le plan de la feuille) et
celui sortant de la feuille vers nous.
La force de Lorentz qui s'applique sur la branche gauche du circuit est suivant . Elle est constante par ailleurs.
Ma difficulté est la suivante : je n'arrive pas à sommer les moments infinitésimaux sur la partie gauche du circuit.
Pour moi, .
J'imagine qu'on obtient en sommant les
(et j'imagine qu'il y a une différence de primitive
à évaluer entre
et
,
étant la longueur de la branche gauche du circuit).
Le problème c'est que pour obtenir cela, il devrait y avoir un . Or, premièrement je n'en ai pas et deuxièmement si j'en avais un il y aurait un souci d'homogénéité (un problème d'unité).
Je n'arrive pas à comprendre comment la somme des moments infinitésimaux sur la branche gauche du circuit s'annulent.
Je souhaiterais si possible passer par un calcul analytique (avec introduction de puis intégrer entre
et
).
Merci par avance,
Je vous souhaite une excellente après-midi.
Bonjour
Tu devrais commencer par faire un schéma soigné de la situation. Ensuite : tu peux considérer que chaque côté est soumis à une force de Laplace de la forme appliquée au milieu de ce côté. Tu as ainsi quatre moments à déterminer. Facile ensuite d'en faire la somme vectorielle. Tu devrais arriver à quelque chose de cohérent avec la notion de moment magnétique.
Merci. Je vais essayer de tirer les choses au clair. Je n'avais pas pris en compte le fait que le moment infinitésimal porte sur une force infinitésimale et non sur la somme des forces infinitésimales.
Merci et bonne journée.
C'est un peu comme pour le poids d'une tige homogène dans le champ de pesanteur homogène. La densité linéique de force (µ : masse linéique) étant la même en tout point de la tige, la moment du poids se calcule comme celui d'une force unique (le poids
) appliquée au centre de la tige.
Ici, dans un champ magnétique uniforme, la densité linéique de force magnétique est uniforme. Le moment de la force de Laplace en un point quelconque se calcule comme le moment de la résultante appliquée au milieu de la tige.
L'analogie avec le moment de la gravité d'une tige, je ne l'ai pas trop saisie. Ce sera peut-être pour plus tard 
Merci pour m'avoir aiguillé sur ma question initiale en tout cas 
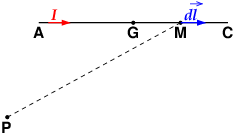
Je veux bien te faire la démonstration générale dans le cas d'une portion rectiligne (AC) de fil conducteur de longueur l placé dans un champ magnétique uniforme de vecteur et parcourue par un courant d'intensité I circulant de A vers C (voir figure).
La force élémentaire exercée sur la portion élémentaire de longueur dl centrée en M, a pour expression :
La résultante de ces force est , en sortant de l'intégrale les termes indépendants de la position du point M :
Le moment en un point P quelconque vaut :
Petite astuce : faire intervenir le milieu G de (AC) :
On développe en sortant les constantes indépendantes de la position de M de l'intégrale :
En effet : je te laisse démontrer, par exemple en raisonnant sur les symétries, que la seconde intégrale est égale au vecteur nul. Cela donne bien le résultat que je t'ai indiqué dans mes messages précédents.