Bonjour kazekage,

je ne peux pas repondre a ton exercice, et personne ne le fera a ma place, pour une simple raison : tu ne poses aucune question ! J'imagine que la question est : "etablir l'equation differentielle du mouvement du pendule en utilisant le theoreme du moment cinetique", mais j'aimerais en avoir une confirmation.
Petite remarque par ailleurs : le repere O,vect(er), vect(e teta), vect(ez) ne s'appelle pas referentiel spherique, mais referentiel cylindrique.
On reprend la discussion des que tu nous dit ce que tu dois faire exactement.

Prbebo.

Merci prbebeo d'avoir quand meme  repondu et donne vie a mon topic.

En verite, la question est sous forme de QCM, et, d'apres l'enonce que je vous ait fourni, on nous demande d'etablir l'expression du moment cinetique  du pendule du professeur tournesol.

Nous avons plusieurs propositions et d'apres la correction, la bonne expression est la suivante : vect(Lo) = mgLcos(teta)vect(ez).

Le probleme c'est que je bloque sur un point qui me parait illogique. D'apres ce que j'ai compris de l'enonce , O est le point d'attache su pendule et M le point ou est attache la masse, d'ou 0M = L, ce qui ne conduirait aucunement a trouver l'expression OM = L x sin(teta).

Donc voila, je ne sais pas s'il y a un probleme dans l'enonce, mais j'aimerais savoir de quelle facon vous auriez aborde le probleme apres avoir applique le theoreme du moment cinetique.

Voila, j'espere avoir rendu ma question un peu plus comprehensible.

Merci de bien vouloir m'aider;

re-bonjour,

j'ai l'impression que tu fais une  sacree salade ! D'abord l'expression que tu donnes "vect(Lo) = mgLcos(teta)vect(ez)." n'est en aucun cas celle d'un moment cinetique. Ensuite, etant donne que la distance OM vaut L d'apres l'enonce, je ne vois pas comment on peut ecrire "OM = L x sin(teta).". Et enfin, puisque tu me reponds on nous demande d'etablir l'expression du moment cinetique  du pendule", le theoreme du mement cinetique n'a rien a voir dans l'excercice...

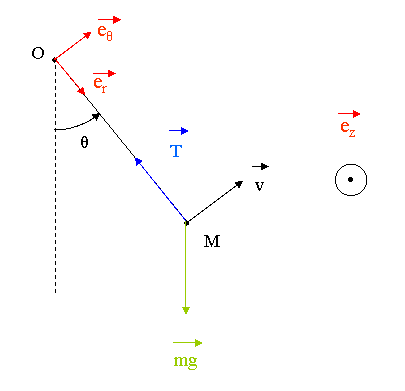
Regarde le schema ci-dessous, qui represente le pendule a la position angulaire avec son vecteur vitesse. J'ai represente aussi les deux vecteurs unitaires er et e, le vecteuir ez etant perpendiculaire au plan du schema. La distqnce OM vaut bien sur L.
Premiere question : peux-tu me donner les expressions du vecteur OM et du vecteur vitesse v projetes dans le repere cylindrique ?
Deuxieme question : quelle est la definition du moment cinetique L par rapport au point O ?

J'attends tes reponmses avant de passer au theoreme.

Prbebo.

Merci beaucoup prbebo,

en effet, j'avais aussi remarque que le corrige qui m'etait fourni avait un probleme.

Vous avez raison, je dois d'abord exprime OM et v projetes dans le repere.

Donc, vu que vect(OM) est dirige selon vect(er), on a vect(OM) = OM.vect(er)

Meme raisonnement avec vect(v), on a vect(v) = v.(vect)eteta

De plus, il me semble que la definition du moment cinetique par rapport a O est la suivante : vect(L) = vect(OM).vect(p) ou vect(p) est la quantite de mouvement M.

Voila, merci beaucoup, si mes reponses sont justes, je pense qu'on peut en arriver au theoreme.

En effet, le vecteur OM s'ecrit OM = L.er (je mets en gras les grandeurs vectorielles).
Trouver que v = v.e n'est pas a proprement parler une performance : j'attendais plutot une expression de la norme v en fonction de ou de sa derivee, soit ici v = L.d/dt.
Le moment cinetique de M par rapport a O est J = OMmv (j'ecris J le moment cinetique pour le distinguer de la lettre L qui represente la longueur du pendule) ; c'est un produit vectoriel donc il est perpendiculaire a OM et a v, cad dirige selon ez (et dans le meme sens selon mon schema). le resultat du calcul donne J = m.L².'.ez ou ' = d/dt. Sais-tu calculer un produit vectoriel ?

Il ne reste plus qu'a appliquer le theoreme du moment cinetique, soit dJ/dt = la somme des moments par rapport a O des forces appliquees au point M. On obtiendra alors l'equation differentielle sur donnant le mouvement de M.

A bientot,  prbebo.