Inscription / Connexion Nouveau Sujet
missile
Bonjour
Un avion situé à la hauteur ha de la mer envoie un missile vers un sous-marin situé à la profondeur hs de la surface de l'eau au moment de l'impact. On admettra que la surface de la mer est absolument plane. On appelle c la distance des projetés orthogonaux de l'avion et du sous-marin à la surface de la mer.
La vitesse du missile est constante V1 dans l'air et V2 dans la mer .
La trajectoire du missile est rectiligne dans les deux milieux et est calculée avec une durée minimum.
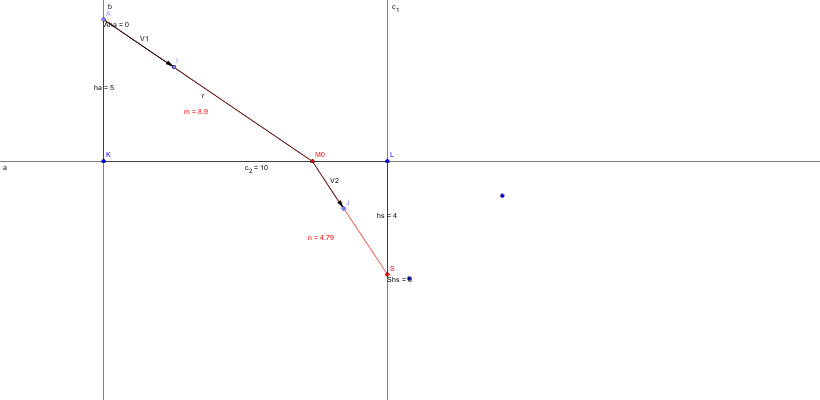
Le problème est de déterminer la position M0 de contact du missile à la surface de la mer.
Déterminer M0 dans les cas suivant :
V1= ha hs c
1.5*V2 5 4 10
2*V2 20 10 30
V2 5 4 10
Montrer qu'il existe une « similitude » avec la loi de la réfraction lors d'un changement de milieu.
Bonjour
C'est un exercice hyperclassique que posent les professeurs de math dès qu'ils ont étudié la notion de dérivée lorsqu'ils sont soucieux de donner à leur enseignement des applications concrètes. Cet exercice est repris au niveau post-bac en optique pour illustrer le principe de Fermat.
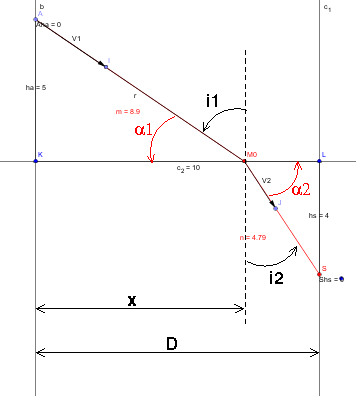
En posant : KMo=x, MoL=D - x avec D = constante =KL, il est facile (Pythagore...) de déterminer en fonction de x, D,ha et hs les distances AMo et MoS puis la durée totale t du parcours de A à S.
En considérant t comme une fonction de x, un calcul de dérivée et un tableau de variation permettent facilement de montrer que la valeur minimale de t est obtenue pour une position particulière de Mo qui vérifie la loi de Descartes sur la réfraction...
Bonjour vanoise
En effet, le but est de montrer que la trajectoire du missile, calculée pour un minimum de temps correspond au trajet de la lumière dans la traversée de deux milieux.
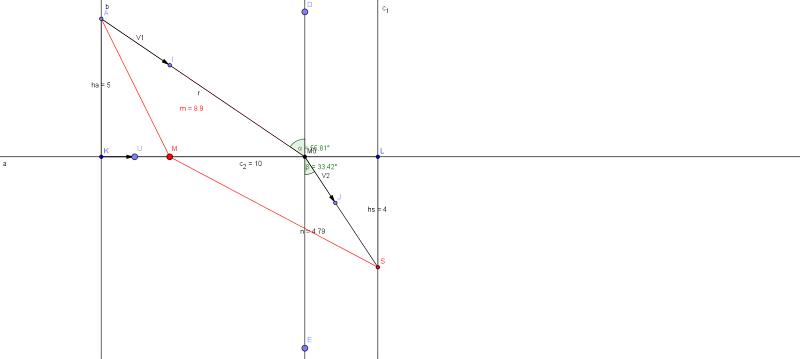
ha, hs, c et k désignent respectivement la hauteur de l'avion au moment du tir du missile, la profondeur du sous-marin, la distance des projetés orthogonaux K et L de l'avion et du sous-marin à la surface de la mer et le rapport des vitesses V1/V2 du missile dans l'air et dans la mer. M est le point d'impact du missile à la surface de la mer.
(un ordinateur tient compte de la vitesse et de la direction du sous-marin)
On prend comme origine K et on appelle c l'abscisse de L et x celle de M sur la droite (KL  ).
).
Il faut chercher la (ou les) position(s) de M telle(s) que S(x)=AM/k + MB est minimum.
On est amené à calculer les zéros de S'(x) = x/kAM - (c - x)/MB
AM =  (ha² + x²) et MB =
(ha² + x²) et MB =  (hs² + (c-x)²)
(hs² + (c-x)²)
Un petit programme donne les résultats suivants :
k ha hs c solution
1.5 5 4 10 7.356393021
2 20 10 30 25.70521133
3 30 20 50 44.25872802
1 5 4 10 50/9 (ligne droite)
La précision est 10 -9 et la 4ième solution est exacte.
Il reste deux problèmes à résoudre: montrer que ces solutions correspondent à des minima (facile) et que s'il existe d'autres solutions, elles ne conviennent pas (moins simple).
On peut essayer de transformer S'(x) = 0 en une équation polynomiale P(x) = 0
dans laquelle P(x) est un polynôme de degré au plus 4.
Maintenant, il reste à montrer le lien avec la formule de Descartes
On appelle M0 le point M correspondant au minimum.
Ce minimum correspond à S' = 0 soit x/kAM0 =(c-x)/M0B (en admettant que M0 est entre K et L )
Ce qui donne x/V1AM0 = (c-x)/V2M0B ou encore v/V1 * x/AM0 = v/V2 * (c-x)/M0B,
en appelant v la vitesse du missile dans le vide .
On désigne n1 = v/V1 et n2 = v/V2 et on a x/AM0 = cos( /2-
/2- 1) = sin (
1) = sin ( 1) et
1) et
(c-x)/M0B = cos(  /2 -
/2 - 2) = sin(
2) = sin( 2) (cf. la figure ci-dessous)
2) (cf. la figure ci-dessous)
Ce qui fait: n1 sin( 1) = n2 sin(
1) = n2 sin( 2) on retrouve
2) on retrouve
la relation de Snell-Descartes