Inscription / Connexion Nouveau Sujet
Miroir de fresnel
Bonjour
Je bloque vraiment sur cet exercice:
On considère dans l'air,2 miroirs plans M1 et M2 formant un dièdre d'arête A et d'angle (pi/2 -
) avec
petit.Une source lumineuse S ponctuelle,monochromatique(de longueur d'onde
),est placée dans le plan bissecteur du dièdre formé par les miroirs,à une distance R de l'arête.On étudie l'interférence entre les 2 ondes suivantes:
La 1ere réfléchie par M1,puis M2,la 2nde réflechie par M2 puis M1.Le plan d 'observation (P) est un écran perpendiculaire au plan bissecteur du dièdre,parallèle à son arête est situé à la distance z de A ().
Déterminer,à l'aide d'une construction geometrique,la region dans laquelle on peut observer des phenomenes d'interference.Montrer que la distance entre les 2 sources qui produisent les franges d'interférence est 4R.
Là je ne sais vraiment pas comment faire...
Merci d'avance pour votre aide
Bonjour
J ai trouvé un lien mais je n'y trouve que l'énoncé..Je n'arrive pas à trouver des relations claires entre les angles .
A l'aide svp..
Bonjour Priam, Bonjour Ariel60,
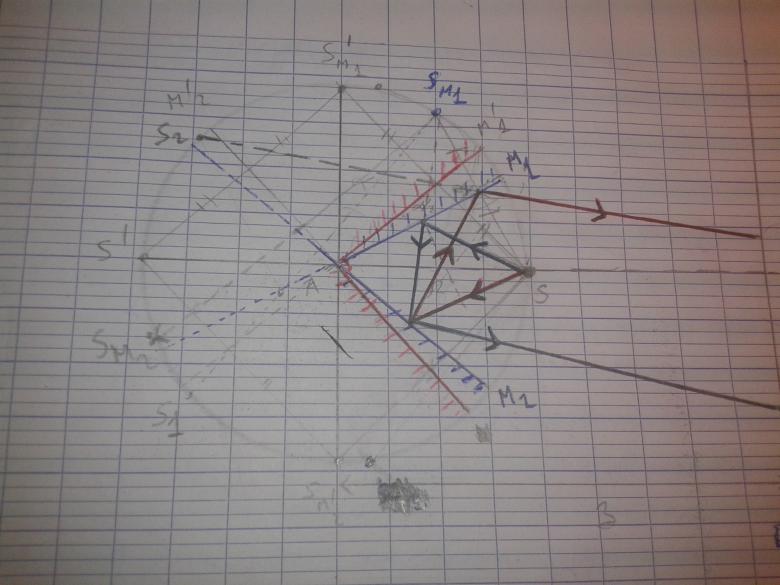
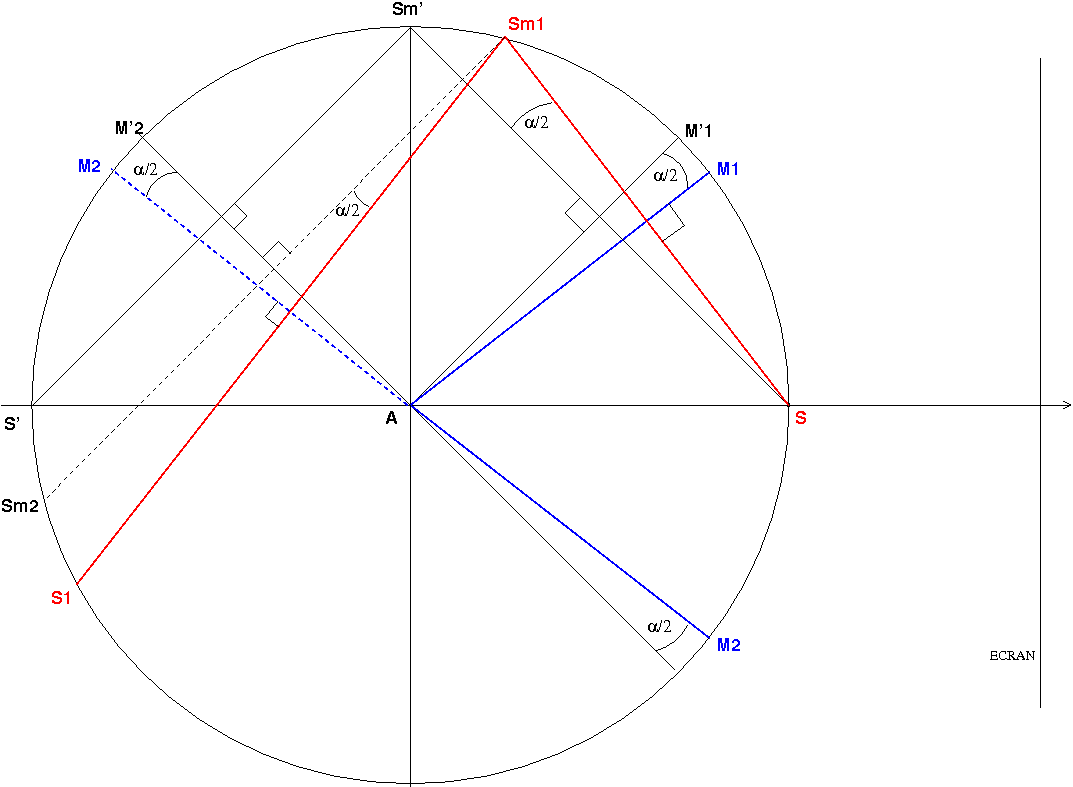
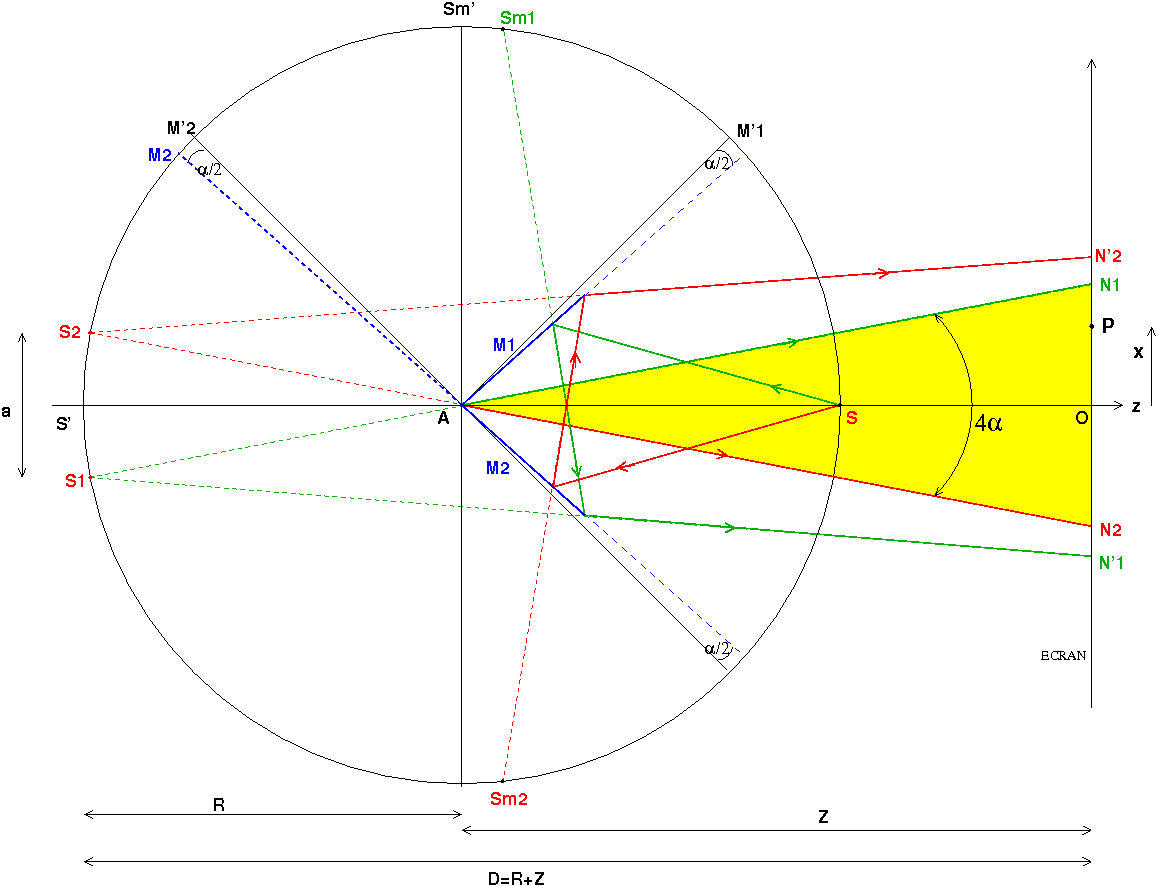
J'avoue ne jamais avoir entendu parler de ce dispositif interférentiel avant de lire ce post. Je n'ai peut-être pas bien cherché mais je n'ai trouvé qu'une seule référence sur internet, sans doute celle évoquée précédemment... J'ai de gros doutes sur la pertinence du montage. Pour obtenir une source lumineuse quasi monochromatique ponctuelle, il faut utiliser un laser avec devant une lentille de très courte focale ou bien une lampe spectrale munie d'un condenseur et d'un diaphragme de faible ouverture . De tels dispositifs sont relativement encombrants et pourtant, il faut les placer entre les miroirs et l'écran d'observation ; compte tenu de la faible largeur du champ d'interférence, aucune chance d'observer des franges à mon avis ! Ariel60 ferait sans doute mieux d'étudier le dispositif classique des miroirs de Fresnel... Cela dit, le problème est intéressant sur le plan géométrique. J'ai commencé par tracer un cercle de centre A et de rayon R = SA. M'1 et M'2 sont des miroirs fictifs orientés exactement à 90° l'un de l'autre. M1 et M2 désignent les deux miroirs (et leurs prolongements) décalés chacun de 
/2 par rapport aux miroirs fictifs précédents. M'1 donnerais de S une image virtuelle Sm', M'2 donnerait de Sm' l'image S' diamétralement opposée à S. Pour ne pas surcharger la figure, je ne me suis pas intéressé au faisceau se réfléchissant d'abord sur M'2 puis sur M'1 : ce faisceau semblerait provenir de la même source virtuelle S' ; ainsi les deux faisceaux pourraient être considérer comme provenant de la même source virtuelle S' ; il n'y aurait donc pas de franges d'interférences possibles avec deux miroirs orthogonaux.
Le rayon issu de S et réfléchi par M1 semble provenir de Sm1, symétrique de S par rapport à M1. Théorème de l'angle au centre : . La longueur de l'arc (Sm' Sm1) est donc R.
. Puisque Sm1Sm2 est parallèle à Sm'S' , la longueur de l'arc (S'Sm2) est aussi R.. En appliquant une deuxième fois le théorème de l'angle au centre, on démontre de même que la longueur de l'arc (Sm2S1) vaut R.. La longueur de l'arc (S'S1) est donc 2R..
On démontre de la même façon que la lumière se réfléchissant d'abord sur M2 puis sur M1 semble provenir d'une source ponctuelle virtuelle S2 , symétrique de S1 par rapport à l'axe (A,z). On obtient bien ainsi le résultat demandé. Bien sûr, en pratique, l'angle est très faible, on peut confondre longueur de l'angle et longueur de la corde. Le dispositif interférentiel est équivalent à deux sources ponctuelles S1 et S2 distante de a=4R., placées symétriquement par rapport à l'axe (A,z), la distance de ces sources à l'écran étant D=R+z.
Il y a peut-être une démonstration plus simple...
La suite est classique...
Bonjour,
Merci encore pour votre explications;mais je ne comprends pas pourquoi Sm2 ne se trouve pas en bas en bas à droite dans le cercle,puisqu'il est l'image de S par rapport à M2,donc symetrique par rapport à M2.D'après ce que j'ai fait en haut sur le schema,j'ai S1S2(longueur de l'arc)=R .Je pose
;avec
Alors mais apres j arrive pas à trouver la valeur de
...
Je me suis intéressé à la lumière émise par la source ponctuelle S qui subit une première réflexion sur M1 puis une seconde réflexion sur M2.
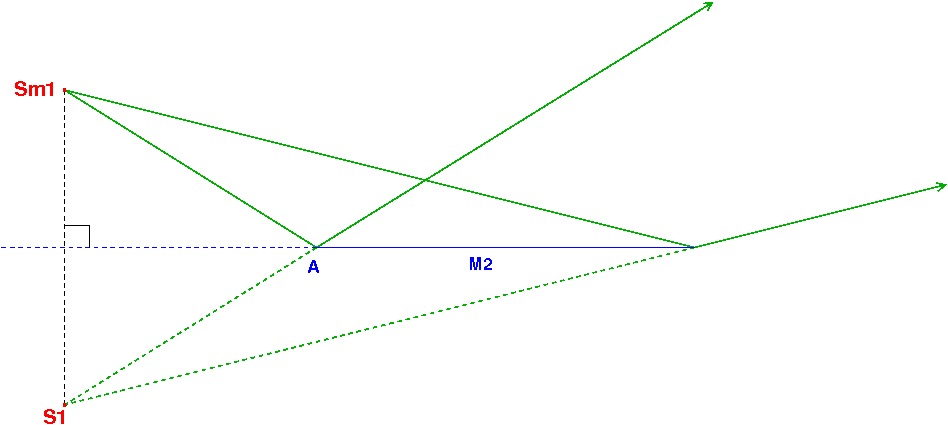
La lumière se propageant vers M2 après la réflexion sur M1 semble venir d'une source fictive (virtuelle) Sm1 : symétrique de S par rapport au plan contenant M1. Après la réflexion sur M2, cette lumière semble provenir d'une source virtuelle S1 : symétrique de Sm1 par rapport au plan contenant le miroir M2. Le point Sm2 n'est qu'un intermédiaire de raisonnement : Sm2 est le symétrique de Sm1 par rapport à M'2, M'2 étant la position de M2 dans le cas particulier =0.
J'utilise un résultat très classique de l'optique géométrique : un miroir plan donne d'un point objet une image virtuelle, symétrique du point objet par rapport au plan contenant le miroir (voir figure ci-dessous où je représente deux rayons réfléchis pour rendre la situation plus concrète).
Je n'ai traité que la moitié du problème. Il faut ensuite considérer la lumière qui se réfléchir d'abord sur M2 et ensuite sur M1 : il faut alors s'intéresser au symétrique de S par rapport à M2 puis considérer le symétrique de ce point par rapport à M1. On obtient un point S2 symétrique de S1 par rapport à l'axe (A,z).
PS : simple curiosité personnelle : cet exercice a-til été donné par ton professeur ou l'as-tu trouvé sur internet ? J'ai expliqué déjà que le montage est totalement irréaliste...
Cet exercice m'a été donné en travaux dirigés par le professeur..J'ai tracé chacun des rayons mais ils ne donnent pas d'intérférences
J'ai tracé chacun des rayons mais ils ne donnent pas d'intérférences
Je crois que tu commets une faute de compréhension et une maladresse. Pour l'incompréhension : il ne faut surtout pas imaginer que, si on trace deux rayons au hasard : l'un se réfléchissant sur M1 puis sur M2 (parcours n° 1), l'autre se réfléchissant d'abord sur M2 puis sur M1 (parcours n° 2), ces deux rayons vont nécessairement se couper sur l'écran. Il faut en revanche démontrer que les deux faisceaux, après les deux réflexions successives dans des ordres différents, présente une partie commune, appelée champ d'interférence. Pour tout point P de ce champ, les deux trajets sont de longueurs différentes : S1P d'une part, S2P d'autre part. Cette différence de marche, dépend de la position du point P : l'éclairement en P dépend donc de la position de P : on observe des franges d'interférences...
Pour la maladresse, elle concerne ton schéma. Pas question évidemment de respecter les proportions réelles :
est de l'ordre du dixième de degré, a=S1S2 est de l'ordre du millimètre, D est de l'ordre du mètre... Il faut un peu d'habitude pour réaliser un schéma clair et démonstratif qui n'induit pas d'idée fausse.
Observe attentivement le schéma joint. J'ai tracé en vert, les rayons extrêmes réfléchis par M1 puis par M2 (parcours n° 1) :
- je me suis d'abord intéressé au rayon qui se réfléchit sur M1 avec un point d'incidence infiniment proche de A. Il se réfléchir sur M2 en un point infiniment proche de A en semblant provenir de S1 : c'est le rayon AN1.
- je me suis ensuite intéressé au rayon issu de S qui se réfléchit sur M1, puis au bord de M2 pour arriver sur l'écran en N'1.
J'ai ensuite réalisé un tracé symétrique (en rouge) pour les rayons se réfléchissant d'abord sur M2 :
- Le rayon incident issu de S se réfléchissant infiniment près de l'arête A se réfléchit sur M1 en semblant provenir de S2 : c'est le rayon AN2.
- Le rayon se réfléchissant sur M2 puis au bord de M1 arrive sur l'écran en N'2.
On constate que le champ d'interférence, c'est à dire la zone commune aux deux faisceaux réfléchis est limité par les rayons AN1 et AN2 (couleur jaune). La largeur du champ d'interférence sur l'écran est ainsi :
N1N2=Z.4R.
.
La suite est très classique...
Cet exercice m'a été donné en travaux dirigés par le professeur
Je te suggère de lui demander comment il est possible de voir des franges sur l'écran sans que le système optique équivalent à la source monochromatique ponctuelle S n'intercepte la lumière réfléchie par les miroirs en direction de l'écran. La largeur du champ d'interférence au voisinage de S est a=4R
, valeur de l'ordre du millimètre. Compte tenu des dimensions de la source (voir mon message du 11-05-17 à 15:16), celle-ci empêche la lumière réfléchie d'atteindre l'écran. Bien sûr, le problème ne se pose pas avec le véritable dispositif des miroirs de Fresnel dans lequel la source est à gauche des miroirs, la lumière se propageant vers la droite... Sa réponse m'intéresse 
... Bref : cet exercice est l'occasion de calculs géométriques intéressants sur le plan théorique mais sans le moindre intérêt pratique...
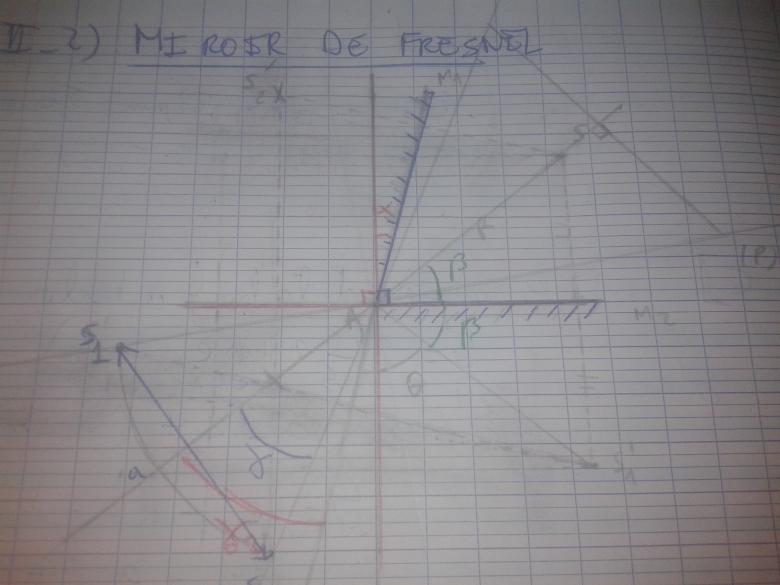
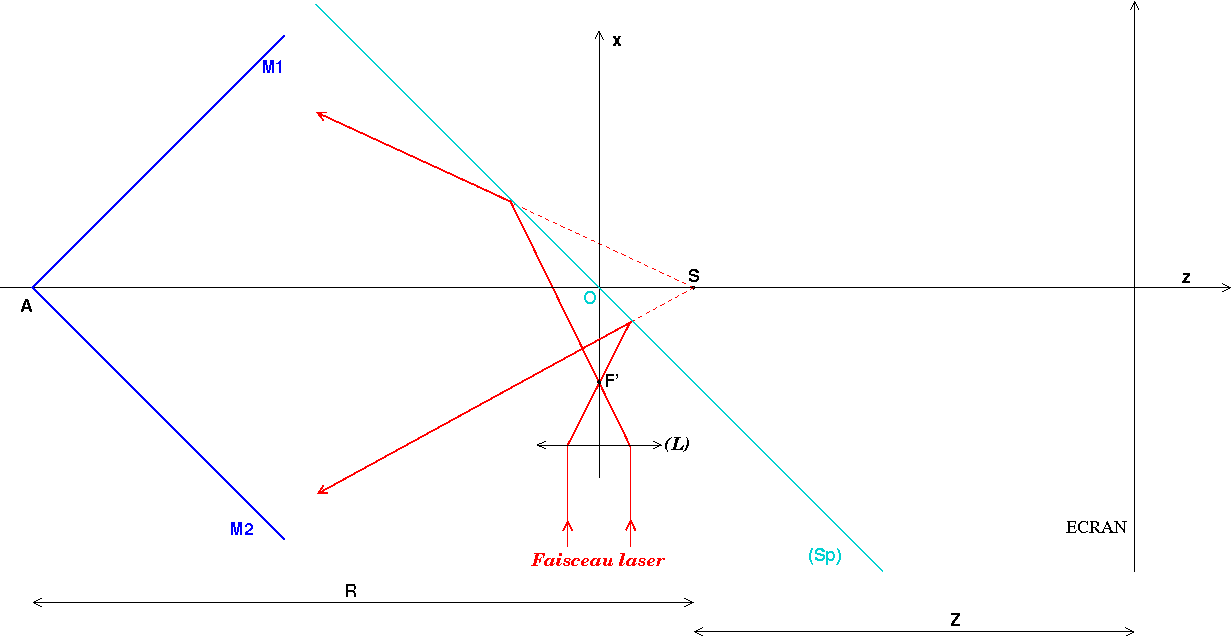
Il y a une parade possible au problème rédhibitoire posé par le positionnement de la source lumineuse entre les miroirs et d'écran d'observation. On décale la source ponctuelle F' (foyer image d'une lentille (L) de courte focale éclairée par un faisceau laser) sur le côté, assez loin de l'axe (Oz) de façon à ne pas gêner la propagation de la lumière entre les miroirs et l'écran et on place une lame séparatrice (Sp) inclinée de 45° par rapport à l'axe (Oz) (la figure n'est pas du tout à l'échelle...). Cette lame à la propriété de réfléchir 50% de la puissance lumineuse incidente et d'en transmettre 50%. La puissance transmise vers les x positifs est ici inutile mais 50% de la puissance incidente est réfléchie vers les miroirs en semblant provenir d'une source ponctuelle S, symétrique de F' par rapport à (Sp) donc sur l'axe (Oz), conformément à ton énoncé. 50% de la puissance réfléchie par les deux miroirs M1 et M2 sera réfléchie par (Sp) dans le sens des x négatifs et sera aussi inutile mais les 50% transmis permettent d'obtenir une figure d'interférence sur l'écran d'observation. Au final : seulement 25% de la puissance lumineuse est utile mais avec un bon laser ou même une lampe spectrale de bonne puissance, les franges d'interférence peuvent être observée dans de bonnes conditions...
Ton énoncé ne parle pas de cela et décrit un dispositif totalement aberrant...
Bonjour,
Merci encore une fois pour les explications et mes excuses pour le retard.Mon prof avait dit qu'on devait juste considérer cet exercice comme un cas idéal alors on ne tient pas compte du dispositif de la source S
Mon prof avait dit qu'on devait juste considérer cet exercice comme un cas idéal alors on ne tient pas compte du dispositif de la source S
Cela s'appelle : "noyer le poisson" au lieu de reconnaître le caractère totalement irréaliste du problème... Mais peut-être que ton professeur n'avait pas détecté la difficulté posée par la position de la source ... Ce n'est pas un hasard si Fresnel, Newton, Young et plus généralement les physiciens qui ont étudiés le phénomène d'interférence lumineuse n'ont pas retenus ce dispositif...
Annuler
connectez vous