Inscription / Connexion Nouveau Sujet
methode de calcul de forces dans un mécanisme parallèle
Bonsoir,
Tout d'abord une petite précision : je viens de sortir d'école d'ingé (plutôt électronique et informatique), et je n'ai plus vraiment fait de mécanique générale depuis la prépa.
J'aurais donc une question assez ouverte : est-ce que quelqu'un pourrait me dire par quelle(s) méthode(s) on calcule les forces que peut transmettre un mécanisme parallèle?
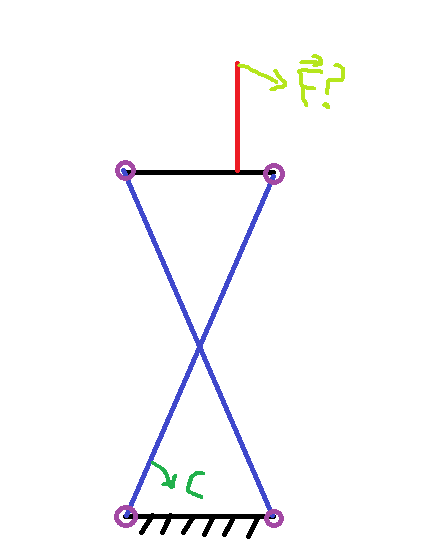
Dans l'immédiat, un bras de mon robot ressemblerait à l'image jointe.
Le bras est constitué de 4 segments, deux à deux de même longueur (reliés par des pivots, représentés par les cercles violets). Le segment noir du bas est fixe par rapport au robot. La barre rouge est fixée au segment noir du haut.
Le but serait d'utiliser un ressort de torsion pour créer un couple C sur l'un des segments bleus, de manière à plaquer le bout du segment rouge contre le mur.
Du coup, mon but serait de calculer la force F qu'exercerait le bout du segment rouge sur le mur, dans une position donnée et en fonction du couple C exercé.
Néanmoins, vu que je risque de rencontrer d'autres problèmes similaires, je serais plus intéressé par des pistes de méthode générale, que par une solution pour ce problème particulier.
En vous remerciant par avance
Sandro
PS : j'ai mis le sujet ici car je pense qu'il doit être au programme des écoles d'ingé de méca, mais si quelqu'un pense qu'il serait mieux ailleurs, ça me vas aussi
Bonsoir
Pour résoudre ce type de problème où les frottements sont négligés, il existe une bonne vieille méthode connue sous le nom de méthode des travaux virtuels. Imagine une rotation élémentaire d'un angle d
. Le couple fournit le travail élémentaire C.d. Cette rotation élémentaire entraîne une translation élémentaire dl ( en vecteur ) de l'extrémité de la tige que tu peux déterminer par un raisonnement géométrique. Le travail élémentaire de la force F est ainsi le produit scalaire F.dl.
En absence de frottement :
F.dl=C.d
Sous toute réserve. Pas sûr d'avoir bien compris le problème avec ce schéma très succinct.
Bonsoir,
et merci.
C'est vrai que c'est beaucoup plus concis comme méthode que ce à quoi j'avais fini par obtenir en écrivant l'équilibre (forces et moments) pour chaque segment.
Par contre, est-ce que la force F est parallèle au vecteur dl? Dans le cas contraire, comment déterminer la composante perpendiculaire à dl?
Merci d'avance et bonne soirée
Sandro
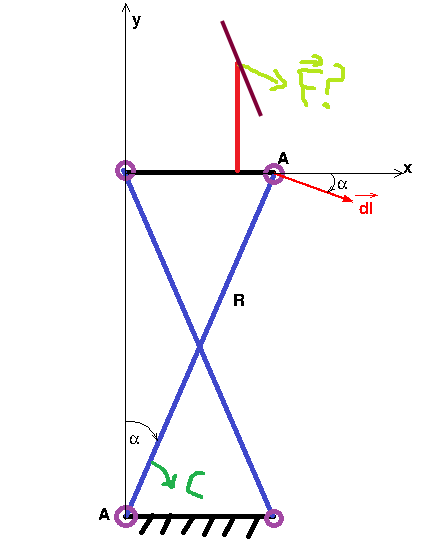
Ton vecteur a effectivement une composante verticale et une composante horizontale. Tu peux exprimer simplement ce vecteur en étudiant le déplacement élémentaire de l'axe de la liaison pivot en haut et à droite du schéma.
Ensuite, en fonction du positionnement par rapport au mur de la barre schématisée en rouge, tu devrais te débrouiller.
J'avoue ne pas trop comprendre où est ce mur...
Bonjour,
Pour le mur, il se trouve "à droite", sachant qu'on suppose être dans une situation où le bout du segment rouge est en appui contre le mur.
Avec la méthode que tu m'as donné, je ne devrais pas avoir trop de mal à calculer .
Je ne devrais pas avoir trop de mal non plus à calculer à l'aide des travaux virtuels.
Par contre, ce que je ne sais pas, c'est si ensuite j'ai le droit de dire que , ou est-ce que [tex]\vec{F}[\tex] a aussi une composante perpendiculaire à [tex]\vec{dl}[\tex]?
Autrement dit, est-ce que la force exercée par le bout de la barre rouge est nécessairement colinéaire avec le déplacement du bout de la barre rouge?
La méthode est beaucoup plus simple que cela !
Le produit scalaire est effectivement simple à exprimer en fonction de la norme F du vecteur force, de d
et de paramètres géométriques du système.
Il suffit alors d'écrire :
Simplification par d et le tour est joué !
J'ai rajouté le mur en marron sur le schéma.
Le but, c'est de déterminer la force avec laquelle le bras vas appuyer sur le mur (le schéma représente le plan x-y, le mur est vertical, et le but est que le robot appuie suffisamment fort contre deux tels murs (avec 8 bras comme celui représenté) pour ne pas glisser vers le bas.
Si jamais ça t'intéresse, j'ai une description du projet complet sur un forum de robotique :
(1er post) et des explications encore plus complètes plus loin dans la discussion :
(sur 3 posts)
Du coup, ce que je souhaiterais, c'est déterminer , dont à priori, je ne sais rien. Avec ta formule, j'en connais la composante selon une direction (celle de
). Mais qu'en est t'il pour la direction orthogonale à
: est-elle nulle? (ça ne me paraîtrait pas absurde, mais je ne connais pas non plus l'argument qui permettrait de l'affirmer)
J'ai un peu complété ton schéma. Le vecteur déplacement virtuel est :
Si tu veux connaître la norme du vecteur force, il faut absolument connaître par un autre raisonnement la direction et le sens de la force F.
Par exemple, si la force est exercée horizontalement vers la droite : ; la formule précédente conduit à :
Par exemple, si la force est verticale ascendante : ; cela conduit à :
Et oui : pour exercer une force orientée vers le haut, il faut exercer un couple tendant à faire tourner la tige AB dans le sens négatif : C<0 dans ce cas.
et si on ajoute des lois de frottement tige/paroi ?
Effectivement : si on connaissant l'orientation du mur : vertical ? horizontal ?
On pourrait alors définir F comme la somme d'une composante normale et d'une composante tangentielle et l'angle entre la normale au mur et le vecteur F serait
tel que :
où f désignerait le coefficient de frottement solide qu'il faudrait estimer en fonction des états de surface respectifs (de l'ordre de 0,3 peut-être ? On pourrait alors obtenir l'angle entre le vecteur F et le vecteur dl pour exprimer le produit scalaire.
Cela mériterait un schéma clair avec un mur clairement défini...
Je me répète : Si tu veux connaître la norme du vecteur force, il faut absolument connaître par un autre raisonnement la direction et le sens de la force F.
Cette autre raisonnement peut effectivement être celui sur les frottements solides.
Merci à vous deux!
Du coup, je n'ai aucun moyen, à priori, de connaître la direction et le sens de F?
Pour les frottements, à priori je partais sur des frottements coulombiens statique (le but est que ça bouge pas).
A la base, je pensais étudier ça séparément (vérifier si la force F+p est dans le cône de frottement, où p est la partie du poids du robot par bras (à priori p=m*g/8), sachant que la gravité est selon l'axe z)
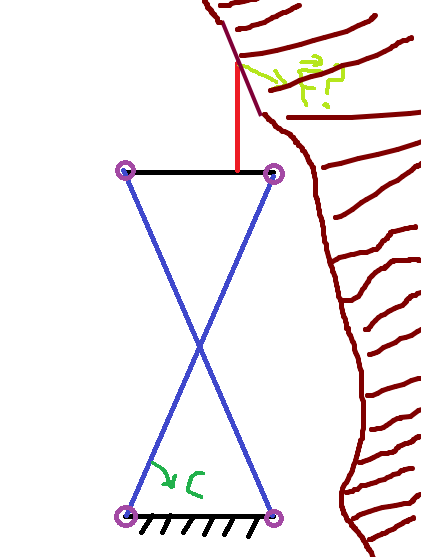
Je suis peut-être un grand imbécile mais je n'ai toujours pas compris l'orientation de ton mur... Comment le représenter sur ton schéma ? Sinon, effectivement, en statique, les lois de Coulomb vont fournir max .
Est-ce que c'est plus clair comme ça? (la partie hachurée est de la roche)
A noté que la plupart du temps le bras sera dans une position avec alpha (celui de ton schéma) plus grand, du coup pas de problème de collision.
Le bout de la barre rouge représente plus précisément le point de contact d'une roue avec la paroi, mais comme cette roue est "fixe" (fixée sur un moteur supposé bloqué), ça ne change rien à priori par rapport à une simple barre
et si on ajoute des lois de frottement tige/paroi ?
Effectivement : si on connaissant l'orientation du mur : vertical ? horizontal ?
On pourrait alors définir F comme la somme d'une composante normale et d'une composante tangentielle et l'angle entre la normale au mur et le vecteur F serait
tel que :
où f désignerait le coefficient de frottement solide qu'il faudrait estimer en fonction des états de surface respectifs (de l'ordre de 0,3 peut-être ? On pourrait alors obtenir l'angle entre le vecteur F et le vecteur dl pour exprimer le produit scalaire.
Cela mériterait un schéma clair avec un mur clairement défini...
Je me répète : Si tu veux connaître la norme du vecteur force, il faut absolument connaître par un autre raisonnement la direction et le sens de la force F.
Cette autre raisonnement peut effectivement être celui sur les frottements solides.
Désolé, j'avais raté ce message.
Pour le mur, en première approximation on peut le considérer parallèle à l'axe y (en pratique j'aurais des approximations de son orientation à partir soit juste de la position des 4 bras présents sur ce mur, soit à l'aide d'un LIDAR).
Par contre, j'ai un doute sur le
Tu as tout à fait raison concernant les frottements . En cas de glissement, tu aurais effectivement . En statique, tu as seulement :
en considérant le coefficient de frottement statique très peu différent du coefficient de frottement dynamique comme écrit dans mon message de 15h55.
Autre chose : ton schéma de 12h54 que j'ai annoté suggère la présence d'un plateau orientable (j'ai peut-être trop d'imagination...) qui viendrait se plaquer sur le mur. Envisager d'utiliser les lois de Coulomb était alors envisageable. Il n'est plus question de ce plateau dans ton schéma de 16h24. Une simple tige venant s'appliquer sur un mur en matière sans doute peu rigide va créer une déformation locale empêchant tout glissement.
Pour pouvoir déterminer F avec précision, il faudrait faire une étude statique complète, ce qui supposerait de connaître les actions du sol aux niveau des axes de liaisons inférieurs. Ces actions sont inconnues...
Donc, sans connaître la direction de F, je pense qu'il faut se contenter d'ordre de grandeurs et de raisonnements qualitatifs.
Pour une force verticale, pour empêcher la voûte de s'écrouler par exemple, il faut un angle faible (sinus au dénominateur) et une valeur de C négative.
Pour une force horizontale orientée vers la droite du schéma, il faut C>0 et un angle plutôt élevé (cosinus au dénominateur).
Autre problème : tu parle de ressort de torsion, type ressort spiral peut-être. Le moment C du couple fourni n'est pas constant, il est plutôt de la forme :
C=k(-o)
où k est une constante caractéristique du ressort et o la valeur de pour laquelle le ressort n'est pas déformé.
Annuler
connectez vous