Bonjour j'aimerais un peu d'aide pour un DM de Physique dont l'énnoncé est le suivant, s'il vous plait  :


Sur un cube de verre d'indice n0, on place une cuve sans fond sontenant un liquide d'indice n<n0. En un point I de l'interface AB , on fait arriver un faisceau lumineux ayant toutes les directions possibles. Les rayons lumineux pénètrent dans le cube et on considère ceux qui sortent par la face BC.

Schéma :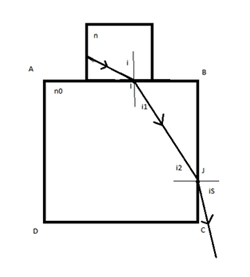

1. Faire une figure montrant la marche des rayons lumineux. Ecrire les lois de Snell-Descartes aux points I et J. Donner une troisième relation entre les angles i1 et i2.

=> J'ai mis n*sin i = n0*sin i1 no*sin i2 = sin iS et i1+i2= pi/2

2.On cherche à établir une condition sur les indices n et n0 pour qu'un faisceau lumineux émerge de la face BC ( la taille du cube est suffisament grande pour ne pas limiter le faisceau lumineux).
-Exprimer l'angle limite de réfraction i2L et écrire la condition sur i2 pour que le faisceau émerge de la face BC .

=> i2L = arcsin (1/n0) car n0>1 et i2<iS (j'ai supposé que le mileu sortant était l'air et que donc son indice était 1 ???) ; donc i2 doit etre inférieur a arcsin (1 / n0 )

-En déduire une inégalité satisfaite par l'angle i et les indices n et n0

=> en calculant j'en ai déduit que i2<arcsin (1/n0) <=> i <arcsin ((1+n0) /n)

-Montrer que la condition d'émergence du faisceau s'écrit n> ou = racine(n0²-1)

=> et la je bloque ! Un petit coup de pouce svp ^^

Edit Coll : image placée sur le serveur de l' Merci d'en faire autant la prochaine fois !