Inscription / Connexion Nouveau Sujet
mélange diphasée
 philou28
philou28Bonjour
Dans une enceinte un volume constant V0 de galium de masse m0 passe d'une température T1 à une température T2. Il n'y a pas d'échange avec l'extérieur.
Les données sont : les pressions de vapeur saturante à T1 et T2 : Ps(T1) et Ps(T2)
Les deux températures T1 et T2.
La fraction massique x1 de vapeur initiale à T1
La fraction massique x2 de vapeur finale à T2
cp(liqu) et cp(vap)
Lv(T1) et Lv(T2)
Il faut calculer le transfert thermique Q reçu par le galium au cours de cette transformation.
Donc comme la transformation est isochore W=0
Donc  U=Q+W=Q=
U=Q+W=Q= H-
H- (PV)=
(PV)= H-(Ps(T2)-Ps(T1)V0
H-(Ps(T2)-Ps(T1)V0
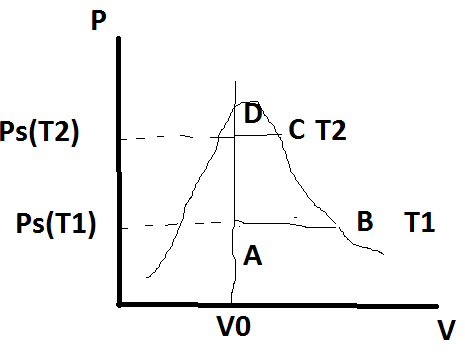
Je pense qu'il faut considérer la transformation ABCD mais je ne vois plus qu'elles formules utiliser pour calculer  H....
H....
Merci pour votre aide
L'expression  U=Q+W=Q=
U=Q+W=Q= H-(
H-( PV)=
PV)= H-(Ps(T2)-Ps(T1)V0
H-(Ps(T2)-Ps(T1)V0
Le chemin que tu choisis pour calculer  H est possible mais pose un problème peut -être pas à ton programme d'ailleurs: la capacité thermique massique de la vapeur saturante le long de la courbe de saturation ne peut pas être assimilée à la constante CP(vap) pour la bonne raison que la pression n'est pas fixe le long de cette courbe et les propriétés thermodynamiques d'un gaz dépendent fortement de la pression.
H est possible mais pose un problème peut -être pas à ton programme d'ailleurs: la capacité thermique massique de la vapeur saturante le long de la courbe de saturation ne peut pas être assimilée à la constante CP(vap) pour la bonne raison que la pression n'est pas fixe le long de cette courbe et les propriétés thermodynamiques d'un gaz dépendent fortement de la pression.
En revanche, la pression, pour peu bien sûr que ses variations ne soient pas trop importantes, influence très peu les propriétés thermodynamiques d'un liquide. Tu peux donc considérer la capacité thermique massique du liquide saturant comme une constante : c 4,18kJ.kg-1.K-1 (sans doute le cp(liq) de ton énoncé). Dans ces conditions, puisque H est une fonction d'état, tu peux calculer
4,18kJ.kg-1.K-1 (sans doute le cp(liq) de ton énoncé). Dans ces conditions, puisque H est une fonction d'état, tu peux calculer  H en imaginant le chemin fictif réversible suivant :
H en imaginant le chemin fictif réversible suivant :
1 : liquifaction isobare et isotherme de la vapeur présente en A :
 H1=-mo.x1.Lv(T1)
H1=-mo.x1.Lv(T1)
2 : échauffement du liquide saturant de T1 à T2 :
 H2=mo.c.(T2-T1)
H2=mo.c.(T2-T1)
3 : vaporisation partielle isobare isotherme de la masse mo.x2
 H3=mo.x2.Lv(T2)
H3=mo.x2.Lv(T2)
En fait j'ai deux cp un liqu qui vaut 0,149 kJ et un cp vap qui vaut 0,100 kJ, ce n'est pas de l'eau, je prend le liqu mais le cp vap ne sert à rien ? sachant qu'il y a un équilibre vapeur liquide ?
Merci beaucoup
Je t'ai fourni par habitude la valeur de c pour l'eau liquide...
Pose ici : c = cp(liq).
Il est possible d'aller de A à D sans faire intervenir d'évolution isobare de la vapeur. On peut donc se passer de la valeur de cp(vap) pour cette question.
Il arrive souvent qu'un énoncé fournisse plus de données numériques qu'il n'est nécessaire. En fait : l'idéal serait de n'en fournir aucune dans l'énoncé et de mettre à disposition de l'étudiant des tables thermodynamiques où il pourrait trouver par lui-même les données utiles...
Il arrive aussi que l'exercice est un petit extrait d'un problème plus long où les données inutiles dans l'extrait sont utiles dans le reste du problème.
Je dois calculer la variation d'entropie pour cette transformation
La formule est  S=Qéchangée/T
S=Qéchangée/T
Je prend le Q trouvé juste avant mais je divise par quelle température T1 ou T2 ?
Merci
Il faut bien revoir ton cours ! la formule que tu indiques n'est valide que pour une transformation réversible et isochore.
Cela s'applique aux transformations 1 et 3 car, pour un mélange diphasé, une transformation isobare est aussi isotherme.
Dans le cas d'une transformation réversible non isotherme, il faut partir de la variation élémentaire :
puis intégrer. Pour l'évolution 2, cela donne :
Remarque préliminaire : il y a une erreur dans l'énoncé tel que tu l'as recopié : l'existence du transfert thermique est en contradiction avec la phrase : Il n'y a pas d'échange avec l'extérieur. Il faut supposer que le récipient indéformable contenant le gallium est diathermane, c'est à dire qu'il est conducteur thermique.
Que veut dire calculer la variation entropique de l'univers ?
"L'univers" désigne ici l'ensemble constitué du gallium, de l'enceinte qui le contient et du milieu ambiant entourant cette enceinte. Ce milieu ambiant est de capacité thermique tellement grande devant celle du gallium qu'il peut échanger de la chaleur avec le gallium sans variation notable de sa température, il se comporte comme un thermostat de température Text. Si le gallium reçoit le transfert thermique Q, le thermostat "reçoit", au sens algébrique du terme, le transfert thermique (-Q). La variation d'entropie du thermostat est :
En notant
 S la variation d'entropie du gallium calculée précédemment, sachant que l'entropie est une fonction d'état extensive, la variation d'entropie de l'univers s'écrit ainsi :
S la variation d'entropie du gallium calculée précédemment, sachant que l'entropie est une fonction d'état extensive, la variation d'entropie de l'univers s'écrit ainsi :
"L'univers" ayant évolué ici de manière adiabatique irréversible à cause du déséquilibre thermique entre le thermostat et le gallium, le second principe impose :
 Su > 0.
Su > 0.
Dans de nombreux problème, on demande de vérifier cette inégalité...
Remarque : il faut considérer ici la capacité thermique de l'enceinte négligeable devant celle du gallium, ce qui ne semble pas précisé dans l'énoncé.
Le thermostat à la température T3 qui chauffe le galium se trouve où dans cette univers ? Cette température c'est la Text ?
N'ayant pas l'énoncé complet, j'ai noté Text (comme extérieure) la température du thermostat. Rien n'empêche de la noter T3 !
Le thermostat est le milieu qui entoure l'enceinte qui contient le gallium, de façon à permettre un transfert thermique entre lui et le gallium. Suivant la valeur de T3, on peut envisager plusieurs situation.
Cas le plus simple : T3 correspond à la température ambiante ; le thermostat est tout simplement l'air ambiant.
Ici, T3 est sans doute nettement supérieur à la température ambiante ; le thermostat peut être un four dans lequel on place l'enceinte contenant le gallium.
Dans d'autres situations, on pourrait envisager qu'un s'agisse d'un congélateur...
Merci pour votre aide
Si  Sunivers >0 il y a création d'entropie.
Sunivers >0 il y a création d'entropie.
Dans les formules quelle est la différence entre les d et les  .
.
Je les utilise mais ce n'est pas absolument claire dans ma tête.
Encore merci
"d" est utilisé pour désigner en math une différentielle ; cela correspond en physique à une variation élémentaire de paramètre ou de fonction d'état : dT, dP, dU, dS,...
" " est utilisé pour désigner une quantité élémentaire : quantité élémentaire de travail, quantité élémentaire de chaleur (transfert thermique) :
" est utilisé pour désigner une quantité élémentaire : quantité élémentaire de travail, quantité élémentaire de chaleur (transfert thermique) :  W,
W,  Q...
Q...
On peut fournir un travail plus ou moins important mais parler de variation de travail n'a pas de sens !
Quand on ait varier une quantité élémentaire entre deux états (deux températures) on alors une variation avec un
entre deux états (deux températures) on alors une variation avec un  ?
?
Le symbole  désigne une variation autre que infinitésimale (variation finie) : variation d'énergie cinétique ou potentielle en mécanique :
désigne une variation autre que infinitésimale (variation finie) : variation d'énergie cinétique ou potentielle en mécanique :  Ec,
Ec,  Ep ; en thermo :
Ep ; en thermo :  U,
U,  H,
H,  S...
S...
Pour désigner une quantité autre que élémentaire (quantité finie obtenue entre deux états), on se contente d'enlever le symbole  devant le symbole de la quantité : quantité de travail : W, quantité de chaleur : Q...
devant le symbole de la quantité : quantité de travail : W, quantité de chaleur : Q...


