Inscription / Connexion Nouveau Sujet
Mécanique vibratoire, systeme sous amorti oscillations forcees
Bonjour,
Je souhaiterais avoir de l'aide sur un problème de mécanique vibratoire.
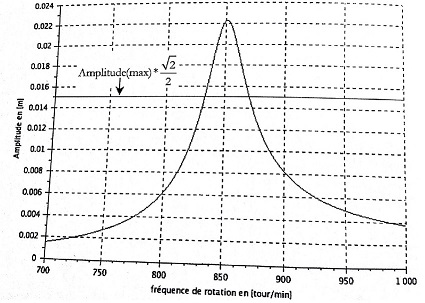
On me donne une courbe et me demande d'en déduire la raideur du système en sachant que c'est un système à un degré de liberté sous amorti en oscillations forcées. Cependant je n'arrive pas à trouver une formule adéquate...
Vous auriez des idées ?
Merci beaucoup.
Bonjour,
Difficile de fournir une réponse précise sans connaître l'énoncé précis. Une indication tout de même. La courbe te permet de connaître la fréquence de résonance (convertis les tours/min en hertz).
La période de résonance (inverse de la fréquence) est très proche de
Salut,
C'est pas évident sans connaitre la force...
Sinon, en supposant que la force vaut 1 Newton sur la plage de fréquences considérée, alors il faut procéder de la manière suivante:
1. Déterminer l'amortissement, appelé facteur de perte hystérétique, par la méthode de la bande passante à -3 dB comme te le suggère le dessin
2. Relever la valeur du déplacement A au niveau du pic de résonance.
3. Estimer la valeur de la raideur en faisant :
Bonjour,
On définit habituellement le facteur de qualité Q de l'oscillateur comme le rapport :
où est la fréquence propre de l'oscillateur, fréquence très proche de la fréquence de résonance lorsque la résonance d'amplitude est relativement aiguë comme ici, et où
représente la largeur de bande passante. Graphiquement, cela donne :
Ce facteur de qualité semble être l'inverse du coefficient introduit par eidos. Dans le cas d'un oscillateur à un degré de liberté, la ” raideur ” est en général le coefficient de raideur d'un ressort défini comme le quotient (Force exercée par le ressort)/(allongement du ressort) ; cette raideur est donc homogène à une intensité de force divisée par une longueur et se mesure en N/m. Or le coefficient K introduit par eidos est homogène à l'inverse d'une distance...
Mais bon : en absence d'un énoncé précis, les ” aidants ” en sont réduits plus à ” jouer aux devinettes ” qu'à faire véritablement de la physique...
C'est vrai qu'il manque de l'information.
En général la courbe qui est tracée est une fonction de transfert et non pas une réponse.
En général cette courbe pourrait correspondre à une réceptance (receptance en anglais, je ne suis pas sûr du mot en français)
La "receptance" s'exprime de la manière suivante pour un système à 1 degré de liberté et pour un amortissement hystérétique :
C'est une fonction complexe. Or à la résonance, vous voyez que les termes de raideur et de masse s'annulent mutuellement. Il ne reste que le terme d'amortissement et qui correspond à la partie imaginaire.
Dans ces conditions, connaissant par la méthode de la bande passante et connaissant
à la résonance (il suffit de lire la valeur sur le graphe), k s'exprime par la relation
et donc en valeur absolu
Bonjour,
Merci beaucoup pour toutes ses réponses, désolé de ne pas avoir donné toutes les infos au début, je ne les avais tout simplement pas (c'est un devoir donné l'année passée que j'essaie de résoudre, j'ai les données au compte goutte).
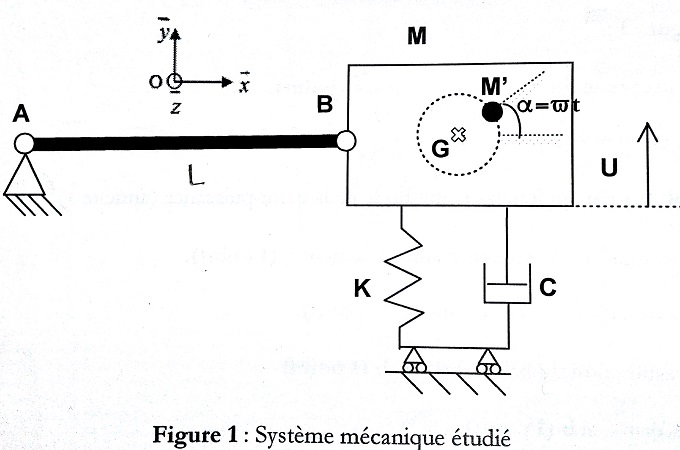
Voici le système étudié.
On me donne les masses du système (la barre AB fait 90kg et la masse M fait 270kg).
L'énoncé demande de trouver la pulsation propre, la raideur et le facteur d'amortissement Zêta.
Bonsoir,
Tu ne donnes pas de renseignement sur M' ?
Quelle est la nature des liaisons mécaniques en A et en B ? Peut-on parler de liaisons pivots parfaites ?
Ce dispositif me gêne un peu : le fait que l'accélération relative de M' par rapport à M possède une composante verticale génère effectivement des vibrations verticales . Cependant, cette accélération relative possède aussi une composante horizontale (de même amplitude d'ailleurs) qui devrait générer des vibrations horizontales. Aucun systèmes d'amortissement de celles-ci ne semble prévu...
Ce schéma devait bien être accompagné d'un texte d'explication et d'un énoncé précis...
On peut peut-être faire des hypothèses à partir desquelles on peut raisonner pour essayer de voir des phénomènes intéressants plus que pour décrire une réalité physique.
La masse qui participe au mouvement de l'oscillateur pourrait être : m =270 +90/2 = 315 kg
M' doit surement être plus petit que m, par conséquent le mouvement de balourd de la masse M' va créer une force excitatrice : ou e est l'excentricité de M' par rapport à l'axe G . Si M' avait été plus lourde que m, alors l'excitation aurait été de type "vitesse" et non pas "force".
Par conséquent il est possible d'écrire une équation correspondant à la courbe :
D'après l'équation qu'avait donné vanoise, il est possible d'en déduire la valeur de k.
La lecture de la courbe à la résonance permet de connaitre la valeur de M'e.
Donc, si la valeur de M' est donnée, on peut en déduire l'excentricité. Si l'excentricité est donnée, on peut en déduire la valeur de la masse M'.
Pour grand (c'est à dire plus grand que la pulsation propre) l'effet de masse prédomine sur le reste, et on voit que la courbe tend vers une asymptote horizontale de valeur
. Cette asymptote est homogène à une longueur, ce qui est bien en concordance avec l'unité indiquée sur la courbe ([m]).
La courbe est donnée en valeur absolu. En réalité la partie réelle de la courbe, pour grand, fait apparaître un signe -. Ce signe - signifie physiquement une opposition de phase entre la force et la déplacement. Lorsque la force agit vers le bas, la masse M se situe au dessus de sa position d'équilibre.
Bonsoir,
La masse qui participe au mouvement de l'oscillateur pourrait être : m =270 +90/2 = 315 kg
Je ne suis pas sûr que les professeurs de fafnouf se contenteront de ce "pourrait". Cela dit, je pense que l'intuition est assez bonne : il est possible de démontrer rigoureusement, en prenant en compte les hypothèses simplificatrices de mon message posté le 22-03-16 à 18:16 que u est solution de l'équation différentielle :
où mT désigne la masse de la tige.
En régime sinusoïdal forcé :
On peut passer aux complexes associés comme cela se fait en électrocinétique des régimes sinusoïdaux. Cela conduit à définir le complexe :
Comme très probablement : M'<<M, on peut poser sans doute : m
 M+mT/2
M+mT/2
L'amplitude des vibrations verticales est le module du complexe précédent et le déphasage
 en est l'argument.
en est l'argument.
La fréquence propre est donc :
La fréquence de résonance d'amplitude est la fréquence qui rend maximum l'amplitude des vibrations Um. Tu pourras démontrer que cette fréquence n'est pas exactement la fréquence propre mais qu'elle en est très proche lorsque, comme ici, la résonance est relativement aiguë.
Désolé : j'ai commis une erreur dans mon message précédent.
Le moment d'inertie de la tige par rapport à son axe de rotation passant par son extrémité A est mTL2/3 et non : mTL2/2...
Cela conduit à faire intervenir mT/3 et non mT/2 dans toutes les équations précédentes.
Je présente mes excuses pour cette étourderie heureusement vite détectée.
Remarque : évidemment, la totalité de mon raisonnement peut être faux si les hypothèses que j'ai posées se révèlent en contradiction avec l'énoncé complet...
Intuitivement parlant, j'ai du mal à croire que la charge de la barre soit répartie 2/3 à gauche et 1/3 à droite.
Le déplacement U est petit devant L . L'angle de rotation de la barre doit donc être très faible. C'est étonnant que cela puisse avoir est une si grande influence.
Si j'imagine deux déménageurs de même taille portant un réfrigérateur, j'ai du mal à croire qu'une petite oscillation des bras de l'un des deux types suffise à faire porter les 2/3 du poids à l'autre.
Bonjour et encore merci pour toutes ces pistes !
En ce qui concerne l'énoncé, il mentionne les deux masses précédemment citées, la masse M' est apparemment de 15g. Il précise également qu'au repos la barre AB est horizontale. Je suppose que les liaisons sont considérées comme parfaites.
En ce qui concerne la courbe, l'énoncé dit que, au moyen d'un capteur de déplacement, on mesure le déplacement U(t) en régime permanent en faisant varier la fréquence angulaire wbarre. La courbe représente alors l'évolution de l'amplitude du déplacement en régime permanent de la masse M.
J'ai calculé l'équation de mouvement (avec b la distance GM'). (toute première question du devoir).
Après c'est tout ce que j'ai, il demande de déduire de la courbe la pulsation propre et la raideur dans un premier temps et ensuite le facteur d'amortissement.
***Formule manuscrite supprimée, merci d'utiliser les outils du forum***
Il y a une manière de savoir quelle est la masse qui participe au mouvement de l'oscillateur, puisque l'énoncé permet de connaitre la valeur de la force du balourd.
Soit F cette force.
Il est possible de connaitre la raideur
En utilisant cette valeur de K et en l'injectant dans la première formule de vanoise qui donnait une expression pour la pulsation propre ,
on peut en déduire la valeur de M :
Si M'=15 g, U=0.022 m et , il suffirait que tu nous communique la valeur de b, pour pouvoir estimer M et voir si cette valeur correspond à 270 + 90/3 kg ...
Il serait tout de même intéressant que fafnouf nous fasse la démonstration de l'équation différentielle :
Intuitivement parlant, j'ai du mal à croire que la charge de la barre soit répartie 2/3 à gauche et 1/3 à droite.
"L'intuition" de eidos se limite à l'aspect statique du problème. Effectivement, on démontre facilement que le raccourcissement du ressort à l'équilibre (noté
 z) vérifie :
z) vérifie :
En revanche l'étude dynamique fait intervenir le théorème du moment dynamique appliqué à la tige et le moment d'inertie de la tige par rapport à l'axe de rotation Az vaut
par conséquent le mouvement de balourd de la masse M' va créer une force excitatrice :
Une force constante, dont d'ailleurs ni la direction ni le sens ne sont précisés, ne peut évidemment pas provoquer de vibrations ! On peut assez facilement démontrer que la force évoquée ici a pour expression :
Cette force tend à provoquer des vibrations verticales mais aussi des vibrations horizontales, d'où mes interrogations du 22-03-16 à 18:16 mais la masse M' étant très faible... La liaison pivot en A est peut-être suffisamment "solide"...
Le rôle de la barre est justement d'empêcher les vibrations dans la direction horizontale. Elle bloque le déplacement horizontal et laisse libre le mouvement vertical. Après je ne vois pas ce que vient faire ici le théorème du moment dynamique. Une masse, c'est toujours statique. La barre est considérée comme un corps infiniment rigide. La barre, en elle-même, d'après les hypothèses, ne vibre pas. La barre n'est pas un corps élastique.
Lorsqu'on raisonne dans l'espace des fréquences, comme c'est le cas ici, l'aspect temporel est toujours sous entendu. D'ailleurs la courbe qui est tracée le prouve bien.
Parmi les différentes méthodes pour retrouver l'équation du mouvement, la méthode des réactances est certainement celle qui est la plus intuitive.
Il faut découpler le système en deux parties : la masse active M' d'un côté et l'oscillateur passif d'un autre de masse .
Les réactances des deux systèmes sont :
et
L'effort de couplage entre les deux systèmes est
Soit
Soit si M' est plus petit que m
Le déplacement de l'oscillateur est donc
Il faut découpler le système en deux parties : la masse active M' d'un côté et l'oscillateur passif d'un autre de masse m=M+m_b/3.
Je n'ai pas vue de démonstration rigoureuse de l'expression de la masse passive, ni des formules qui suivent d'ailleurs...
C'est quoi le but ? Aligner des équations ou bien comprendre la physique des vibrations?
L'idée derrière tout cela est très simple : On découple le système en une partie active et une partie passive, puis on regarde ce qui se passe lorsqu'on le couple.
La partie active c'est le balourd tout seul. Il vibre avec une certaine amplitude égale à son excentricité. Par contre on ne peut rien dire sur la force qu'il exerce puisqu'il est découplé. Une force a toujours besoin de s'exercer "sur quelque chose". Cependant, la connaissance de sa masse nous permet de déduire une autre propriété sur le balourd, à savoir sa réactance (qui est une forme d'impédance si l'on veut)
La partie passive c'est tout le reste, qui est au repos lorsque le système est découplé.
Nous pouvons dans ce cas aussi connaitre la réactance
La réactance répond à la question suivante : Quel est le déplacement du système si je lui applique une force de 1N ?
Ensuite il faut coupler les deux systèmes. Il faut alors appliquer des conditions de continuité entre les deux systèmes, à savoir que la somme des forces au point de contact est nulle et qu'il y a égalité des vitesses.
et
A partir de là, tout est dit, le reste n'est que calcul.
Bonsoir fafnouf,
Il serait tout de même intéressant que fafnouf nous fasse la démonstration de l'équation différentielle
Désolé pour cette phrase : lorsque je l'ai écrite, je n'avais pas compris que tu avais déjà été capable de démontrer l'équation différentielle du mouvement. Bravo ! Ce n'est pas vraiment évident et cela demande un bon niveau en méca ! Tu as dû bien rigoler en lisant certains propos concernant l'influence de la masse de la tige sur le mouvement vibratoire !
Pour tes questions concernant les caractéristiques de l'oscillateur, j'ai réalisé une démonstration que tu trouveras sur le fichier joint : les valeurs de fo, k, C et M'.b sont calculées à partir de renseignements déduits de la courbe de résonance. Les calculs sont très détaillées de façon à être abordable dès le niveau (bac+1).
J'ai trouvé un petit problème au niveau numérique. La valeur M' = 15g me semble nettement trop faible : la valeur de b obtenue à partir de la détermination du produit M'.b me parait trop élevée...
Mes notations ne sont pas nécessairement celles de ton cours mais comme elles sont clairement précisées, tu devrais t'y retrouver.
Voici le lien :
Wow, le rapport de vanoise est incroyable ! Et tu fais ça gratuitement ?
Alors là, je comprends mieux ce que veut dire le mot "rigoureux"...
Quelle chance pour les élèves et le site de t'avoir à leur disposition.
Wahou merci beaucoup Vanoise !!  En effet j'ai fait toute la démonstration pour l'équation de mouvement mais c'était un peu long c'est pour ça que j'avais juste mis la solution ^^ Et maintenant avec ton rapport c'est tout bon !
En effet j'ai fait toute la démonstration pour l'équation de mouvement mais c'était un peu long c'est pour ça que j'avais juste mis la solution ^^ Et maintenant avec ton rapport c'est tout bon !
Encore merci !
et merci aussi Eidos ^^
Bonjour,
De rien, fafnouf ! J'ai aussi trouvé une autre incohérence du point de vue numérique : la valeur de k déduite de la pulsation de résonance, conduit à une valeur du raccourcissement du ressort à l'équilibre à mon avis beaucoup trop faible...
Puisque j'avais fait la démonstration de l'expression de l'équation différentielle avant d'avoir compris que tu avais réussi à l'obtenir, autant la poster sur le forum : elle pourra éventuellement intéresser d'autres personnes... Il s'agit évidemment d'une méthode possible parmi d'autres...
Voici donc le fichier précédent complété par la démonstration.
![]()
C'est juste hallucinant.
A partir d'une simple question mal posée, vanoise, tu as écrit une correction de 10 pages!
Je me demande si tu es fou ou si tu es un génie.
En tout cas, chapeau bas.
Sinon comme tu le disais, la valeur de 15 g pour la masse M' parait faible en effet. Le rapport des masses est . Or la résonance telle qu'elle est définie n'entraîne une amplification que de 1000.
Donc si la masse se déplace de 2,2 cm (comme indiqué sur le graphique), alors l'excentricité devrait être de 2,2*20 000/1000=44 cm.
Cela semble un peu grand en effet.


