Inscription / Connexion Nouveau Sujet
Mécanique statique
Bonjour,
J'ai examen écrit de physique lundi et malheureusement, il y a un exercice que je n'arrive pas à résoudre. Il s'agit d'un exercice d'examen d'une année antérieure (donc important).
Voici l'énoncé : "Un expérimentateur désire déterminer la position du centre de gravité d'une tige hétérogène dont le poids W est de 100 N. Pour ce faire, il attache la tige à l'aide de deux cordes en prenant soin de placer la tige horizontalement. Il mesure alors un angle 
de 36,9° et un angle 
de 53,1°. Si la tige a une longueur de 6,1 m, calcule
a) la position du centre de gravité
b) les forces de tension dans les cordes"
Le prof a donné les réponses : F1 = 80 N et F2 = 60 N et x = 2,196 m.
J'ai essayé de faire l'exercice mais je n'arrive jamais à la bonne réponse. Je joins le schéma que j'ai fait de la situation (je le pense correct) et mon raisonnement (il doit y avoir une erreur quelque part...). Si quelqu'un sait m'aider, ça serait sympa 
** image supprimée **
Merci d'avance,
Yohan
***Edit gbm : seule l'image du schéma peut être postées via le bouton Img. Ta proposition est à recopier***
Bonsoir,
Je vais tenter de te répondre sans avoir la figure...
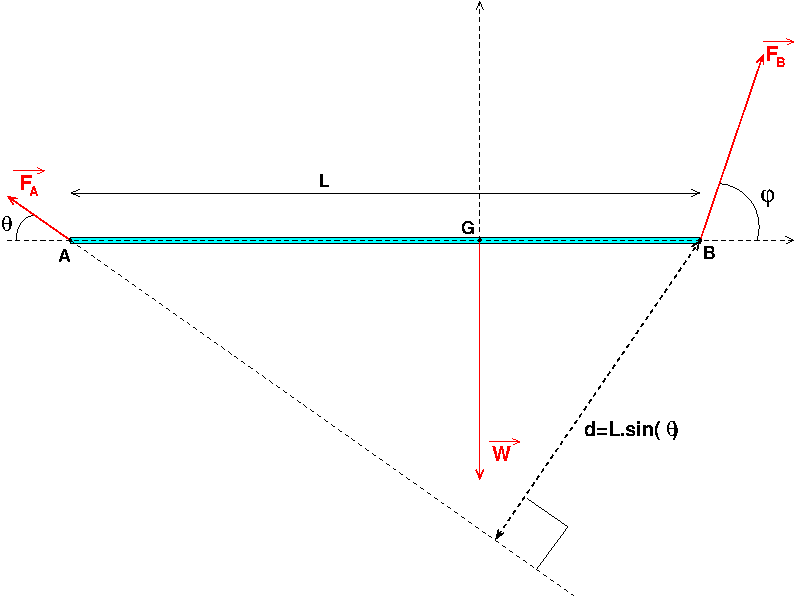
Je note A l'extrémité de la tige à laquelle est fixée la corde inclinée de l'angle ; cette corde exerce sur la tige la force FA ; je note B l'autre extrémité de la tige à laquelle est fixée l'autre corde exerçant sur la tige la force FB.
La somme des trois vecteurs forces est le vecteur nul.
En projection sur un axe vertical, cela conduit à :
W=FA.sin( + FB.sin()
En projection sur un axe horizontal, cela conduit à :
FA.cos() = FB.cos()
Cela donne un système de deux équations à deux inconnues. En remplaçant dans la première FB par son expression déduite de la seconde, on obtient :
La seconde relation conduit à :
Pour la distance AG, il faut appliquer le théorème des moments soit en A, soit en B, soit en G. Appliquons-le en B en écrivant que la somme des moments des trois forces en B est nulle. Soit en utilisant la notion de moment vectoriel (produit vectoriel) soit en utilisant la notion de bras de levier, tu obtiens :
Soit :
Annuler
connectez vous