Deux blocs (m1 = 2 kg et m2 = 3 kg) sont suspendus à une poulie de rayon R  = 20 cm et de masse M = 5 kg par une corde de masse négligeable.
(a) Quelle est  l'accélération angulaire de la poulie ?
(b) Quelle est la tension dans la corde reliant la masse m1 à la poulie ?
(c) Quelle est la tension dans la corde reliant la masse m2 à la poulie ?

Pour la (a) :

J'ai appliqué la somme des moments égale au produit du moment d'inertie par le rayon au carré.
Cependant je me retrouve avec une équation en fonction de T1 et T2 dont on me demande les valeurs dans les questions suivantes, il faudrait
donc passer par une autre méthode mais la quelle ?

Bonjour,
"J'ai appliqué la somme des moments égale au produit du moment d'inertie par le rayon au carré."...
J'aurais plutôt dit : M = J ''.
Non ?

Oui, c'est ce que j'ai fais. Et je me suis trompé dans la phrase...

Avec teta l'accélération angulaire. Cependant, j'ai toujours mon problème avec les tensions.

Oui, c'est bizarre... Mais je ne connais pas d'autre moyen de le faire...
Il est étrange que l'on demande ensuite les tensions dans la corde.

Et pour les calculer avant ? Il y a un moyen ?

Il y a 2 kg d'un côté et 3 kg de l'autre... Il n'est pas difficile de trouver la résultante.
Mais il n'empêche que je ne sais pas ce que viennent faire les deux dernières questions ...
Ou alors il y a un "truc" que je n'ai pas vu... Ce qui peut arriver, personne n'est infaillible.

Je me retrouve avec :

Ö=R(T1-T2-P1+P2)/I

J'ai pensé a T1 = -P2 et T2 = -P1, mais lors de la vérification le résultat est incorrecte !
Je ne vois pas en quoi peut m'aider la résultante du coup, de plus je ne vois pas non plus ce que ça peut bien faire dans le réel.
Pourtant j'ai accroché deux poids à mon lustre...

L'ordre des questions semble correcte car la suite des exercices est créé sur le même principe (ou tous les exos sont faux).

Si j'ai bien compris, il y a deux masses de 2 kg et de 3 kg reliés par une corde et la corde est posée dans la gorge de la poulie...
Si on considère le point en haut de la poulie, il y a une force horizontale de 2g N vers la gauche par exemple et une force horizontale de 3g N vers la droite. La résultante, c'est 1g N vers la droite. Cette force, multipliée par le rayon de la poulie, crée un moment (9.81 x 0,2). La poulie va tourner dans le sens des aiguilles d'une montre... Cela va s'arrêter quand le poids de 2 kg va venir se bloquer sur la poulie ou sortir de la poulie...
Si c'est nécessaire, je ferai un schéma mais, bon, ça va me prendre un moment ...  

Je comprends sans schéma

On se retrouve alors avec 1 moment, mais le calcul est toujours faux.

I = 0.2²*5

Pour information je dois tomber sur ö=6.53 rad/s

Ma formule semble pourtant correct car quand je la teste avec les réponses ça marche... Cependant il faut comprendre

'' = 6,53 rd.s^-2...
Oui, là, il va falloir réfléchir... Il y a une erreur quelque part...
Cela me semble cohérent pourtant...

Ma réflexion n'a toujours rien donné...

Je suis dans le même cas dans l'exercice suivant.

les tensions sur les masses m1 et m2 ont pour expression
T2=m2(g-a)
T1=m1(g+a)
La poulie va tourner dans le sens anti-horaire.
Les forces qui s'exercent tangentiellement à la poulie on la valeur des tensions
Si on attribue le signe + à ce sens ,la somme des moments des forces appliquées à la poulie est
Mts =T2R-T1R
                   =[m2(g-a) -m1(g+a)].R
or a=.R  (accélération angulaire)
d'autre part
Mts=J
avec Mts poour "moments" et accélération angulaire
en développant j'ai obtenu =2g/15R =6,53 rad.s^-2
on peut alors calculer a ,et T1 et T2
T1=22.2N   T2=25,5N
sauf erreur

Ah oui !... L'accélération angulaire s'ajoute à g d'un côté et se retranche de l'autre ...

a n'est pas l'accélération angulaire mais linéaire.
a=R
est l'accélération angulaire

Merci pour ton aide,

Je n'est pas la propriété dans le cour qui permet d'ajouter l'accélération linéaire à celle de g.

Cependant je tombe toujours sur :

ö= g/(R*10)

Je vais bien finir par trouver avec tout ce que tu m'a donné ! Merci

Désolé, on le peut pas éditer :

"Je n'ai pas la propriété"

on a
+=m1
et
+=m2.

Si on projette sur des axes orientés dans le sens du mouvement,on obtient:
T1-P=m1.a  soit T1=m1(g+a)
P-T2=m2.a  soit T2=m2.(g-a)

Je me suis laissé avoir par le message de Marc35 alors que j'aurais pu le trouver seul...

[m2(g-a) -m1(g+a)].R=R²MÖ
<=>
m2(g-a) -m1(g+a) = RMÖ
<=>
g(m2-m1) = RMÖ +m2RÖ + m1RÖ
<=>
g(m2-m1) = Ö R(M+m2 + m1)
<=>
Ö= [g(m2-m1)]/[R(M+m2+m1)]

avec m2-m1 = 1 et M + m2 + m1 = 10

Et pourtant j'ai refais le calcul.

le moment d'inertie d'un disque plein est MR²/2

a)

Force motrice = (3-2)*g = 9,81 N

Soit mi la masse inerte de la poulie ramenée au muvement linéaire.
(1/2).J.w² = (1/2).mi.v²
avec w = v/R et J = (1/2)M.R² (si la poulie peur être considérée comme un cylindre homogène).
(1/2).(1/2)M.R².v²/R² = (1/2).mi.v²
(1/2)M = mi
mi = 2,5 kg

Masse inertie totale : mi + m1 + m2 = 2,5 + 2 + 3 = 7,5 kg

F = ma
9,81 = 7,5 a
a = 1,308 m/s² (accélération des masses m1 et m2)

gamma = a/R = 1,308/0,2 = 6,54 rad/s² (accélération angulaire de la poulie)
-----
b)
T1 = m1*(g + a)
T1 = 2 * (9,81 + 1,308) = 22,2 N
-----
c)
T2 = m2*(g - a)
T2 = 3*(9,81 - 1,308) = 22,5 N
-----
Sauf distraction.  

Sur le schéma T2 est sur la masse 1 et T1 sur la masse2 ?

D'après vos calculs c'est l'inverse. Donc si on prend le sens anti horaire T2 est négatif et T1 positif ce qui n'est pas le cas dans les calculs.

Problème de projection ?

Tu n'aimes pas ma solution ?  

Autre méthode.

Si la masse m1 descend de x, la masse m2 descend de x
Variation d'énergie potentielle de la masse m1 : E1 = -m1.g.x = -2*9,81*x = -19,62x J
Variation d'énergie potentielle de la masse m2 : E2 = m2.g.x = 3*9,81*x = 29,43x J

Soit v la vitesse atteinte par les masses lorsque les masses ont bougé de la distance x.
La vitesse angulaire de la poulie est w = v/R

Energie cinétique de m1 : Ec1 = (1/2).m1.v² = (1/2)*2*v² = v² J
Energie cinétique de m2 : Ec2 = (1/2).m2.v² = (1/2)*3*v² = (3/2)v² J
Energie cinétique de la poulie: EC3 = (1/2)J.w² = (1/2)*[(1/2).M.R²]*w² = (1/4).M.R²*(v)²/R² =(1/4)*M*v² = (1/4)*5*v² = 1,25v² J

L'énergie cinétique totale du système masses + poulie est : Ec = v² + (3/2)v² + 1,25v² = 3,75 v²

Par le principe de conservation de l'énergie mécanique du système, on a donc :

29,43x - 19,62x = 3,75 v²
9,81 x = 3,75 v²

Et comme le mouvement des masses est uniformément accéléré, on a: x = at²/2 et v = at -->

9,81 * at²/2 = 3,75. a²t²
9,81/2 = 3,75.a
a = 1,308 m/s² (avec a l'accélération des masses.)

L'accélération angulaire de la poulie est gamma = a/R = 1,308/0,2 = 6,54 m/s²

...

La méthode précédente (du message du 17-01-09 à 13:00) donne la même réponse mais bien plus rapidement

Hum, j'avais pensé mais comme tu le dis en utilisant l'autre méthode c'est plus rapide.

Par contre ça ne résout pas mon problème : Bien qu'on doit prendre T1 négatif et T2 positif, si on projet dans le sens positif prédéfinit c'est normalement l'inverse non ?

Tu as déjà vu des cordes capables de pousser une charge ?

Avec une corde on ne peut que tirer et pas pousser.

Si T1 et T2 sont les tensions dans les 2 brins de la corde agissant sur les masses, ils sont forcément de même signe puisque la corde reste tendue (T1 et T2 sont dirigés vers le haut).

Le signe dans les calculs dépend du sens positif choisi pour le mouvement.

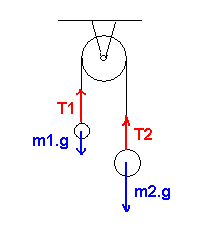
Merci pour le schéma

Regarde :

Je choisis le sens des aiguille d'une montre comme sens positif.

Quand j'applique la somme des moments (T1-T2)R = IÖ

T2 est négatif car il va dans le sens opposé, pourtant dans les calculs on a fait :

(T2-T1)R = IÖ

La nuit porte conseil ^^.
J'ai compris, et j'ai pu faire l'exercice suivant qui est un peu plus dur.

Merci à tous !