Inscription / Connexion Nouveau Sujet
Mécanique du solide
Bonjour à tous,
Je suis en train de faire un exercice sur un variateur de vitesse minidrive :
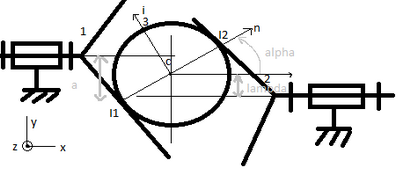
On a un repère x,y et z. La masse est le solide noté 0. Le repère x,y,z est relié au bâti 0.
Les solides 1 et 2 représentent les plateaux coniques.
Le solide 3, une bille de centre C.
On a l'angle alpha = (x,n)
On pose 
1/0 = 
10 x ( vecteur x ).
On pose aussi 2/0 = 20 x.
= O2C
Voilà, le shéma est donné 
1. La première question : Donner V(I2,1/0) en fonction de 10, a, , R et 
.
J'ai donc fait, V(I1,1/0) = V01,1/0 + 1/0 
O1C+CI1.
= vecteur nul + x (-a )y + Rn.
= (-a)z + R ( xn )
Or je ne sais pas ce que vaut le produit vectorielle de x n :/
Merci de bien vouloir m'aider
D'accord, je pense que c'est ça, puisque je dois trouver une relation entre alpha, R, a et w1/0. D'ailleurs, ma relation, est elle bonne sur mon premier message ? ( en remplaçant x^n par sin alpha )
Et en deuxième question : Traduire la relation de roulement sans glissement en I1. En déduire, par décomposition, l'expression de V(I1,3/0).
J'ai dit que comme on avait un roulement sans frottement, alors on a V(I1,3/1) = vecteur nul !
Donc V(I1,3/0) = V(I1,3/1) + V(I1, 1/0 )
Et bien devient V(I1,3/0) = V(I1, 1/0 ).
Est ce bien cela ?
Salut,
a priori la relation donnée au départ est juste par contre je n'avais pas vu que tu bossait en vecteur donc
x n = IIxII*IInII* sin alpha * z
2) oui ça me paraît bon
D'accord
Oui je travail avec des vecteurs, je sais pas trop comment faire pour les mettre.
La suite des questions 3) et 4), c'est la même chose que l'on demande, mais cette fois-ci en I2.
Donc je trouve V(I2,2/0) = w2/0(lambda.z ^ R sin alpha z ) = V(I2,3/0).
En 5) on nous dit que le mouvement 3/0:
- le vecteur omega 3/0 est quelconque
- V(C,3/0) = vecteur nul.
Démontrer que V(I1,3/0) = - V(I2,3/0).
J'ai dit que les vitesses I1 et I2 se compensent pour que le système soit stable. Si elles ne se compensent pas, on a pas de contrôle des solildes 1 et 2 sur le solide 3 et il y aurait un glissement.
Donc V(I1,1/0) + V(I2,2/0) = 0 Or V(I1, 1/0 ) = V(I1, 3/0 , de même pour l'autre, sauf que c'est I2.
Donc en remplaçant, je trouve ce qu'il y a à démontrer.
Est ce bon ce raisonnement ?
Enfin, c'est la dernière question, on demande le rapport r = omega20/omega10.
Et là, je sais pas par quoi remplacer les omega. Je pensais à remplacer omega10 par -w1/0(a-lambda)/Rsin alpha. En reprenant les résultats des autres questions ?
Annuler
connectez vous