Inscription / Connexion Nouveau Sujet
Mécanique du point - Ressort et perle. Equation du second degré.
Bonjour à touuuus... (Je viens déprimer parce que bon, j'avais presque fini mon message quand, par fausse manip, j'ai éteint le PC =_=. *boulet* XD).
Je viens quérir votre aide pour des exercices de physique qui, après deux semaines de recherches intenses, finissent par me sortir par les yeux. Je n'arrive à rien et... bon. Le problème est essentiellement que je n'arrive pas à commencer ni à savoir si je pars dans la bonne direction. Et cela a un énorme impact sur mon travail. Je n'avance pas.
Voilà l'exercice en question...
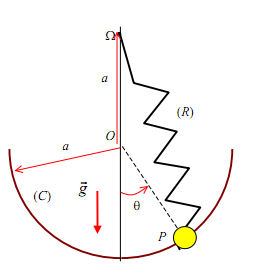
Nous avons là une perle P de masse m lié à un ressort d'origine 
. On nomme k le coefficient de proportionnalité du ressort et l0 sa longueur à vide. Le demi cercle décrit par la perle a un rayon égal à a.
la première question était de trouver l'expression de la force de rappel du ressort en fonction de 
(t), a, l0 et k.
J'ai trouvé : T = -k(2*a*sin() - l0)cos(/2) (ur) + k(2*a*sin() - l0)sin(/2) (u).
La seconde question est de trouver l'équation différentielle du second ordre décrivant le mouvement de la perle (et ce par deux méthodes).
J'ai pensé utiliser la première avec la méthode des petits angles.
Exprimer le poids P en fonction du repère polaire puis d'appliquer le PFD : P + T = m*a
Ensuite projeter sur les deux axes et simplifier les sin(). Seulement problème : on trouve un ² qui m'empêche de progresser.
Savez-vous quelle serait la technique pour se débarrasser des carrés ou alors m'y serais-je mal prise ?
la seconde méthode, on m'a conseillée d'utiliser le théorème du moment cinétique mais là encore... petit problème.
la troisième et dernière question est de trouver une intégrale première puis l'expression du travail de la force exercée par le ressort sur la perle entre 0 et (t). Mais n'ayant pas fait les questions précédentes en entier, je n'y ai pas encore touché.
Cependant, je pense que pour la première partie de la troisième question, il faudrait multiplier par la dérivée preière de ? Cela simplifierait surement le calcul. Mais je verrais ensuite.
Je vous remercie d'avance pour le temps que vous pouvez passer pour m'aider ^^.
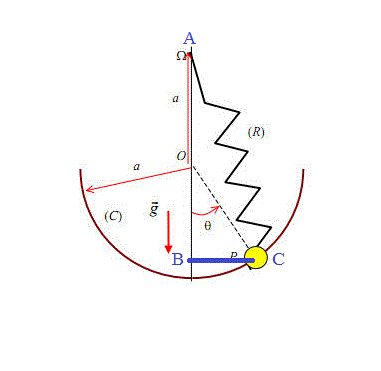
Avec L la longueur du ressort :
AC² = AB² + BC²
AB = AO + OB = a + a.cos(theta)
BC = OC.sin(theta) = a.sin(theta)
--->
(L(theta))² = (a + a.cos(theta))² + a².sin²(theta)
(L(theta))² = a².[(1 + cos(theta))² + sin²(theta)]
(L(theta))² = a².(1 + cos²(theta) + 2cos(theta) + sin²(theta))
(L(theta))² = a².(2 + 2cos(theta))
(L(theta))² = 2a².(1 + cos(theta))
L(theta) = V2.a.V(1+cos(theta))
|Fressort| = k.[V2.a.V(1+cos(theta)) - Lo] (Avec V pour racine carrée).
---
Sauf distraction. 
Merci pour ce calcul. Je me demande pourquoi je n'ai pas le même en utilisant la formule de la longueur d'une corde ?
J'ai ensuite alors votre réponse mais le cos() me gêne dans mes simplifications. Je peux bien remplacer cos() par son équivalent sinus ( 1-2*sin²(/2) ) mais sous une racine carrée, ce n'est guère efficace u_u.
Pour trouver l'équation décrivant le mouvement de la perle :
(Référentiel terrestre).
Energie élastique du ressort : E(theta) = 1/2.k(L(theta) - Lo)² = 1/2.k.[V2.a.V(1+cos(theta)) - Lo]²
Energie potentielle de pesanteur de la bille (altitude de comme référence) : Ep(theta) = -m.g.a.cos(theta)
Energie cinétique de la bille : Ec(theta) = 1/2.J.w² = 1/2 . m.a².(dtheta/dt)²
Si on peut négliger les frottements et la masse du ressort, la conservation de l'énergie mécanique du système ressort + perle permet d'écrire :
E(theta) + Ep(theta) + Ec(theta) = constante.
1/2.k.[V2.a.V(1+cos(theta)) - Lo]² -m.g.a.cos(theta) + 1/2 . m.a².(dtheta/dt)² = 0
On dérive par rapport au temps :
[1/2.k.2.[V2.a.V(1+cos(theta)) - Lo].V2.a.(-sin(theta)/(2V(1+cos(theta))) +m.g.a.sin(theta)].dtheta/dt + 1/2 . m.a².2.(dtheta/dt).(d²theta/dt²) = 0
Et comme dtheta/dt n'est pas nul -->
[1/2.k.2.[V2.a.V(1+cos(theta)) - Lo].V2.a.(-sin(theta)/(2V(1+cos(theta))) +m.g.a.sin(theta)] + 1/2 . m.a².2.(d²theta/dt²) = 0
[-(1/V2).a.k.(V2.a.V(1+cos(theta)) - Lo).sin(theta)/(V(1+cos(theta))) +m.g.a.sin(theta)] + m.a²(d²theta/dt²) = 0
-a².k.sin(theta) + (1/V2).Lo.a.k.sin(theta)/(V(1+cos(theta))) +m.g.a.sin(theta) + m.a².d²theta/dt² = 0
d²theta/dt² = -(g/a).sin(theta) + (k/m).sin(theta) - (1/V2).Lo.k/(am) .sin(theta)/(V(1+cos(theta)))
d²theta/dt² = ((k/m)-(g/a)).sin(theta) - (1/V2).Lo.k/(am) .sin(theta)/(V(1+cos(theta)))
d²theta/dt² = ((k/m)-(g/a)).sin(theta) - Lo.k/(am) .sin(theta/2)
Equation différentielle du second ordre décrivant le mouvement de la perle.
-----
Je n'ai évidemment rien vérifié ...
Youpii !!
Fiou, après quelques minutes de réflexions intenses et de révisions de trigo, j'ai enfin réussi ce que je voulais faire pour la seconde question !
J'ai recalculé la longueur AC de mon côté pour trouver exactement la même chose (je me suis dit que je partais alors bien xD). Puis j'ai fait le PFD avec T + P = m*a et en jouant avec la trigo pour simplifier le )" alt="sqrt(2*(1+cos(
)" class="tex" /> en 2*cos(/2), je suis arrivée à la même équation différentielle que vous avez trouvé en passant par l'énergie ! Donc je pense que c'est bon. ^^
Merci beaucoup pour m'avoir aidée !
La question demeure toujours : où me suis-je trompée pour mon précédent calcul de L ? Je n'obtenais pas les racines comme on les a trouvées en passant par la projection...
Pour la troisième question, est-ce une bonne méthode que de passer par la multiplication par d/dt de chaque côté de l'équation ?
vu que la fonction LaTeX est plus compliquée que ce que je pensais, le truc incompréhensible est en fait V(2*(1+cos))=2*cos(/2)
Par la relation bien connue : cos(2x) = 2cos²(x) - 1
Avec x = theta/2, on a: cos(theta) = 2cos²(theta/2) - 1
2 cos²(theta/2) = (1 + cos(theta))
4 cos²(theta/2) = 2.(1 + cos(theta))
2*|cos(theta/2)| = V[2.(1 + cos(theta))] (1)
Dans l'exercice (voir dessin), theta peut varier dans [-Pi/2 ; Pi/2] et donc theta/2 varie dans [-Pi/4 ; Pi/4] ---> cos(theta/2) > 0 et on a alors |cos(theta/2)| = cos(theta/2)
Et alors (1) devient :
2*cos(theta/2) = V[2.(1 + cos(theta))]
Oui ^^ Tout comme. C'est ce que j'ai fait pour simplifier =).
J'ai réussi à boucler la question 2 comme ça ^^.
Je suis en train de finir la dernière question.
Pour la première partie qui est de trouver l'intégrale première, j'ai multiplié chacun des membres par d/dt puis ensuite j'ai "primitivé".
J'ai trouvé : 1/2*(d/dt)² = (g/a - k/m)*cos() + (2*l0*k)/(m*a) * cos(/2).
Cependant je remarque quelque chose... varie entre [0 ; -
] mais pas entre [-/2 ; /2], non ?
Non.
Avec OC horizontal, la bille le plus à gauche possible sur le dessin, theta = - Pi/2
Avec OC vertical, la bille le plus bas possible sur le dessin, theta = 0
Avec OC horizontal, la bille le plus à droite possible sur le dessin, theta = + Pi/2
theta varie dans [-Pi/2 ; Pi/2]
Annuler
connectez vous