Inscription / Connexion Nouveau Sujet
Mécanique du point plan incliné
Bonjour,
On me propose l'énoncé suivant:
"On étudie le mouvement de M dans le repère (A,Ux',Uy'). À l'instant t = 0, M se
trouve en A avec une vitesse Va = Va Ux'. On note L = AB,  s et
s et  d les coefficients de frottement statique et dynamique, respectivement, entre M et la piste."
d les coefficients de frottement statique et dynamique, respectivement, entre M et la piste."
La situation est schématisée sur l'image attachée.
1) Donner l'expression du poids P et de la réaction F appliqués à M dans (Ux',Uy').
2) En appliquant la deuxième loi de Newton, déterminer l'équation du mouvement entre A et B.
3) Déterminer v(t) et x'(t) pour ( =
=  /4)
/4)
On gardera par la suite cette valeur de 
4) On suppose que la vitesse initiale de M ne lui permet pas d'atteindre le point B et on note F le point le plus haut atteint sur la portion AB. Soit x'F l'abscisse de ce point sur l'axe Ax'. Déterminer x'F. À quelle condition M reste t-il immobile à cette position ?
5) En déduire une relation entre Va, L et  d (et éventuellement d'autre paramètres) pour que M puisse atteindre le point B.
d (et éventuellement d'autre paramètres) pour que M puisse atteindre le point B.
6) On suppose maintenant que la vitesse initiale de M est suffisante pour qu'il puisse atteindre B avec une vitesse finie. Donner l'expression du déplacement élémentaire dr. En déduire le travail des différentes forces entre A et B.
7) Utiliser le théorème de l'énergie cinétique pour calculer la vitesse de M en B.
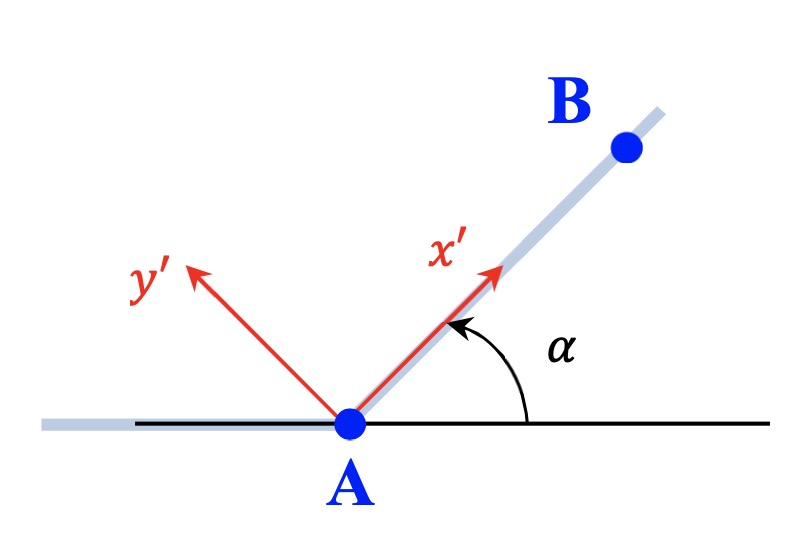
Pour la question 1:
J'ai utilisé le schéma suivant pour projeter les forces.
J'ai trouvé:
N = N Uy'
T = -T Ux'
P = -mgsin Ux' -mgcos
Ux' -mgcos Uy'
Uy'
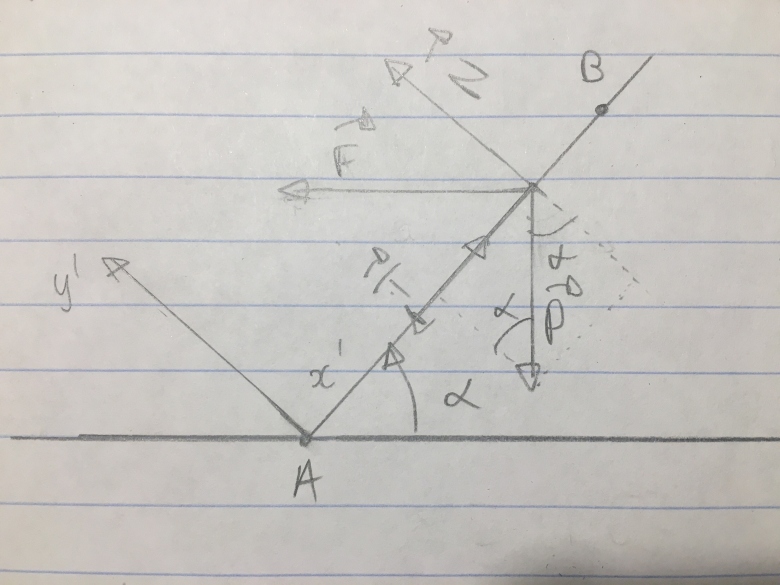
Pour la question 2:
J'ai appliqué la 2ème loi de Newton;
Selon l'axe y':
J'ai indiqué qu'il n'y a pas de mouvement dans la direction de y' donc:
may' = 0 , cela nous permet de trouver: N = mgcos
Selon l'axe x':
max' = -mgsin - T
- T
Lorsqu'il y a mouvement, on sait que T =  dN
dN
Donc: T =  dmgcos
dmgcos
Ainsi:
max' = -mgsin -
-  dmgcos
dmgcos
ax' = g(sin -
-  dcos
dcos )
)
Est-ce bien correct?
Pour la question 3:
Pour V(t):
J'ai indiqué que: V(t=0) = Va
En integrant le résultat de la question 2, j'obtiens:
Vx'(t) = Va - g(sin +
+  dcos
dcos )t
)t
Comme  =
=  /4 rad. On a:
/4 rad. On a:
Vx'(t) = Va - g(sqrt(2)/2)(1+ d)t
d)t
Pour x'(t):
En intégrant la vitesse par rapport au temps et en prenant x'(A) = 0, j'obtiens:
x'(t) = Vat - (sqrt(2)/4)g(1+ d)t^2
d)t^2
Est- ce bien cela?
Je vais m'arrêter là et attendre une réponse de votre part pour poster mon raisonnement pour le reste de l'exercice car cela ferait trop d'un coup ^^ 
Bonjour,
Jusque là, je ne vois pas de problème.
C'est clairement rédigé.
Une faute de frappe avant dernière ligne de 08:03 corrigée après ; ax' = g(-sin - dcos)
Merci pour votre réponse et mes excuses pour la faute de frappe.
Pour la question 4:
Les calculs se font relativement long donc je préfère, si cela est possible, vous envoyez des photos de ma rédaction au brouillon.
Pour déterminer l'abscisse x'F:
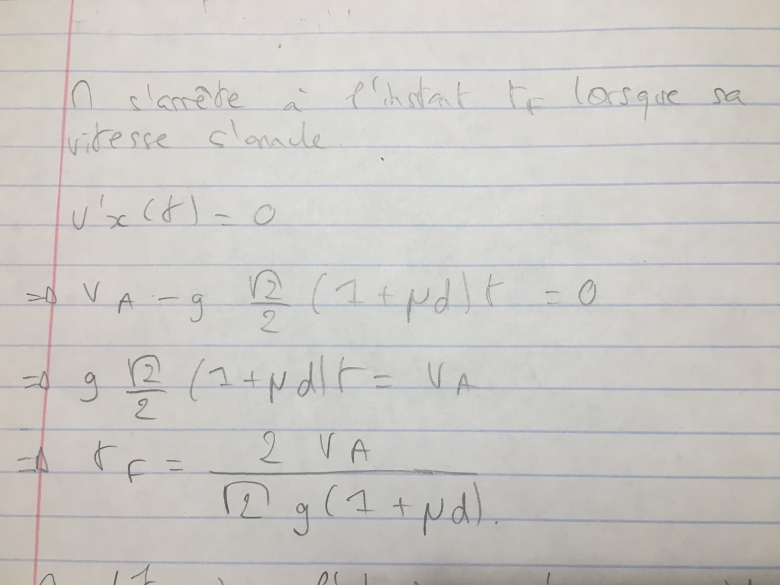
J'essaierai d'appliquer la méthode énergétique pour confirmer mon résultat et m'entraîner avec ce type de raisonnement.
Merci pour la correction, je vais rectifier cela.
Pour la question 5:
On a: AB = L
M atteint B si x'(tF)  L
L
On remplace:
sqrt(2)Va^2/2g(1+ d)
d)  L
L
sqrt(2)Va^2/2gL(1+ d)
d)  1
1
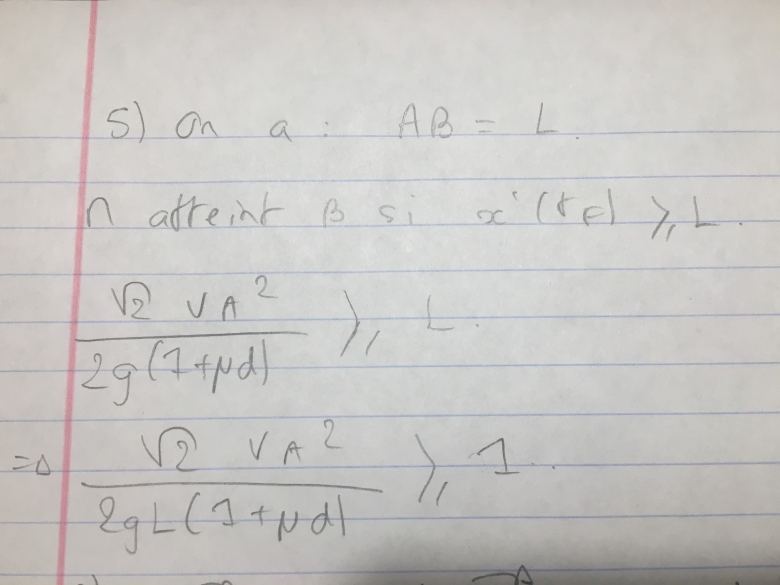
Pour la question 6:
dr = dx' Ux'
Le travail de N est nul car N est perpendiculaire à la trajectoire en tout temps.
Pour le travail de T:
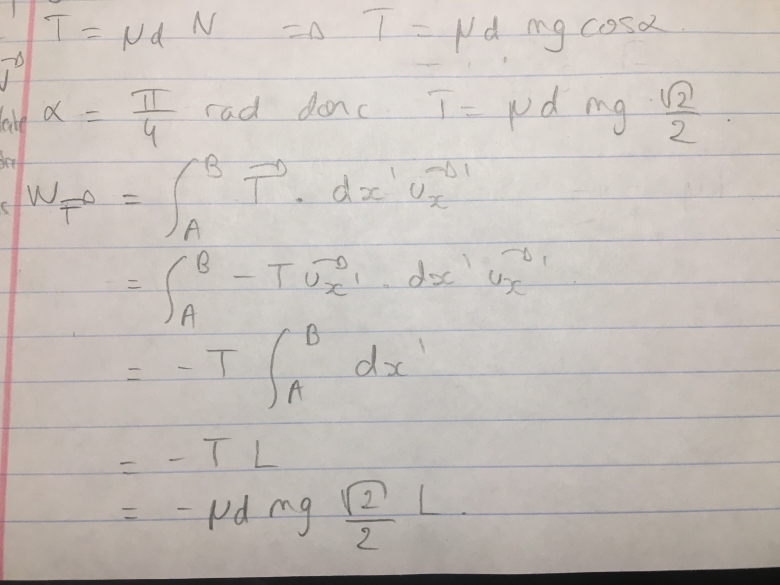

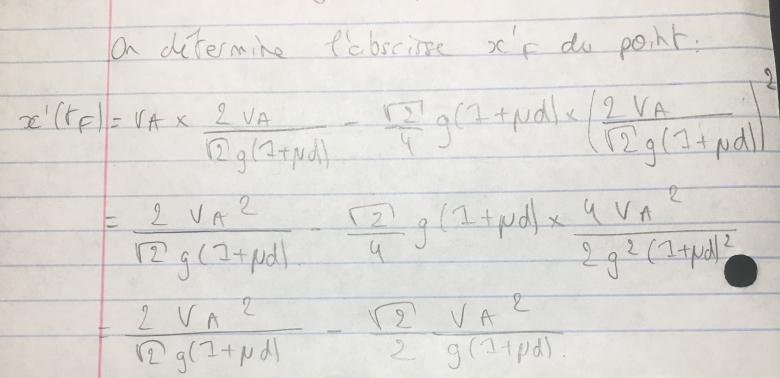
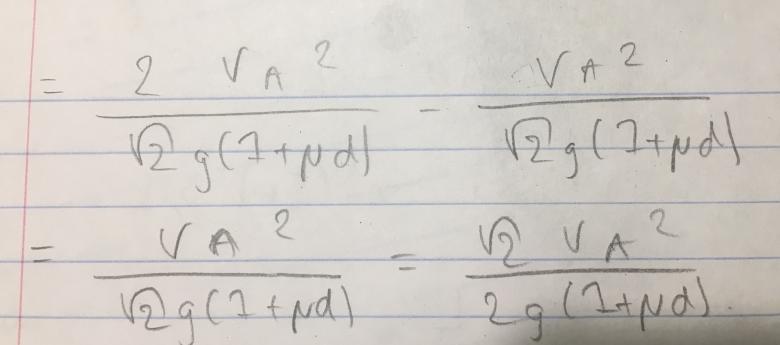
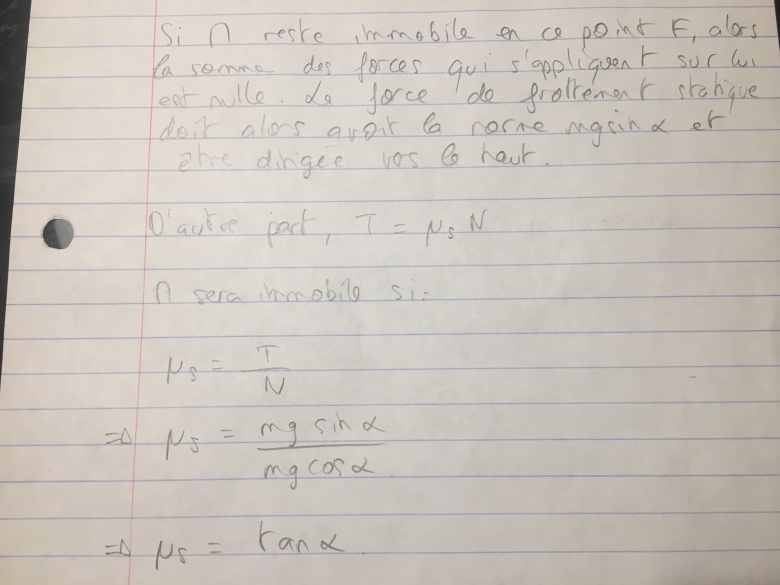
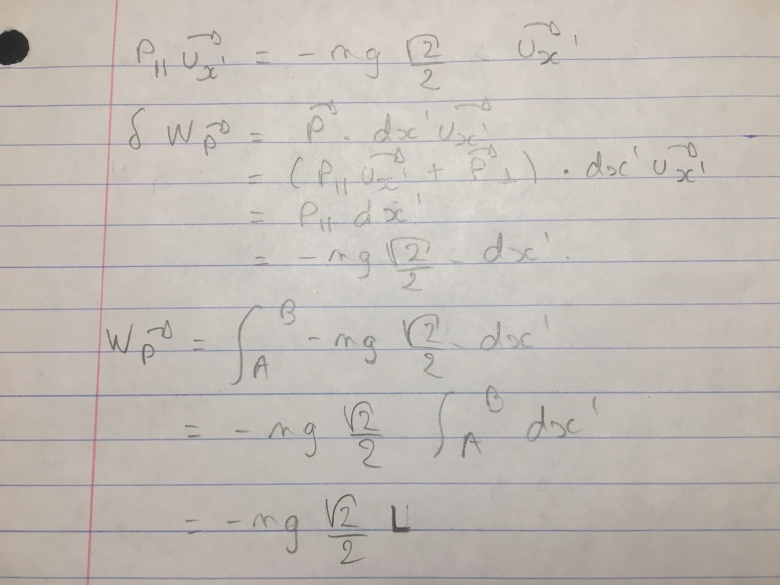
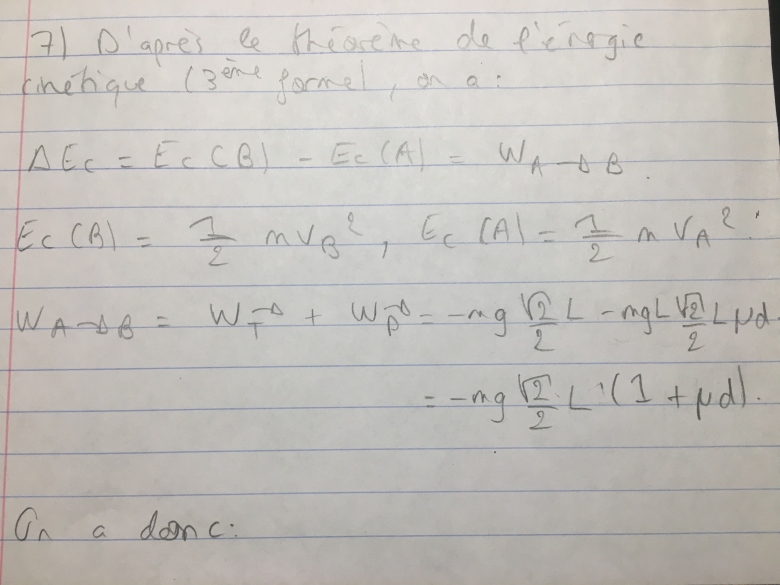
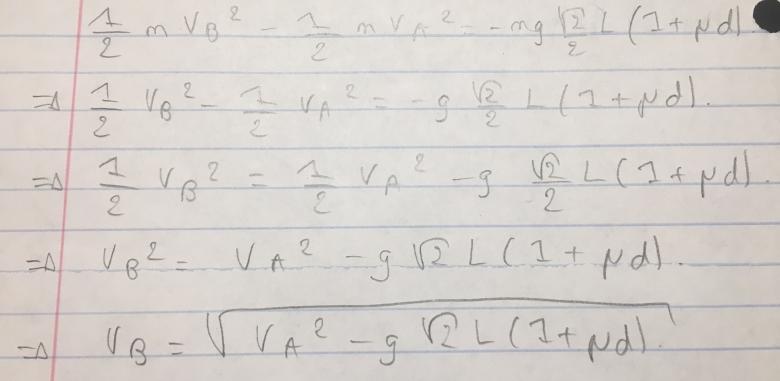

 guide latex
guide latex présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le  mode d'emploi du forum
mode d'emploi du forum
