Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Mécanique du point matériel

Posté par
bissinyandoup 09-06-17 à 20:33

Bonsoir !
S'il vous plait j'ai eu des problèmes sur cet exercice et je souhaite vraiment de l'aide. Voilà l'énoncé :
On donne les équations horaires du mouvement d'un mobile
x=acoswt, y=asinwt et z=bt avec a,b et w des constantes.
1)déterminer les équations polaires les plus simples en coordonnées cylindriques et sphériques.
2) calculer la distance réellement parcouru par le mobile entre les 0 et 2π/w
Bon j'ai pas eu de problèmes avec les coordonnées cylindriques.
En sphériques j'ai eu un problème au niveau du calcul de la distance.
1) r=(x2+ y2+z2)1/2=(a2+b2t2)1/2
=wt
tg=a/bt
2) L=(b2t(a2+b2t2)-1+w2-ab(b2t2+a)-2)1/2dt

Posté par
vanoisere : Mécanique du point matériel 09-06-17 à 20:47

Bonjour
Tu a ici les coordonnées cartésiennes (x,y,z) correspondant à un mouvement hélicoïdal (mouvement en hélice). Le passage en coordonnées cylindrique est intéressant ; le passage en coordonnées sphériques ne présente aucun intérêt.
Un sujet analogue a déjà été étudié sur ce forum ici :
Mécanique du point matériel
Pose des questions précises sur ce que tu ne comprends pas !

Posté par
bissinyandoupre : Mécanique du point matériel 09-06-17 à 20:49

C'est intégré ça qui me dépasse

Posté par
bissinyandoupre : Mécanique du point matériel 09-06-17 à 20:51

Pour avoir L il faut intégrer l'expression la. Et c'est ça qui me dépasse

Posté par
vanoisere : Mécanique du point matériel 10-06-17 à 00:01

Les coordonnées cylindriques du point mobiles à la date t sont :
r=a (constante positive)
=.t
z=b.t=(b/).
Le vecteur déplacement élémentaire peut s'écrire :

\overrightarrow{dl}=r.d\theta.\overrightarrow{u_{\theta}}+dz.\overrightarrow{u_{z}}=a.d\theta.\overrightarrow{u_{\theta}}+\frac{b}{\omega}.d\theta.\overrightarrow{u_{z}}
Les deux vecteur unitaires étant orthogonaux, je te laisse exprimer la norme dl du vecteur déplacement élémentaire puis intégrer le résultat sur un tour...

Posté par
bissinyandoupre : Mécanique du point matériel 10-06-17 à 08:16

Écoute Vanoise, j'ai pas de problème avec les coordonnées cylindriques. C'est en sphériques que j'ai un problème qui est de calculer l'intégrale ci dessous.
En sphériques on a:
L=dM.   dM  étant la norme du vecteur déplacement élémentaire. Après avoir calculer ce déplacement, je remplace dans la formule utilisé pour calculer la distance et j'obtiens :
L=[b4t2(a2+b2t)-1+a2b2(a2+b2t2)(b2t2+a)-2+(a2+b2t2)w2sin2wt]dt. Mon problème est que je n'arrive pas a intégrer ça. J'aimerais que tu m'aide à faire cette integration s'il te plaît.

Posté par
vanoisere : Mécanique du point matériel 10-06-17 à 12:02

Citation :
déterminer les équations polaires les plus simples en coordonnées cylindriques et sphériques.

Es-tu bien sûr de ton énoncé ? Puisqu'il est question de choisir les coordonnées les plus simples, il s'agit logiquement des coordonnées cylindriques ou des coordonnées sphériques.
Ce genre de coordonnées est là pour simplifier les calculs, pas pour les compliquer ! Si tu avais à étudier, par exemple, le mouvement d'un petit bateau à la surface des océans, tu aurais intérêt à choisir les coordonnées sphériques mais pas ici !
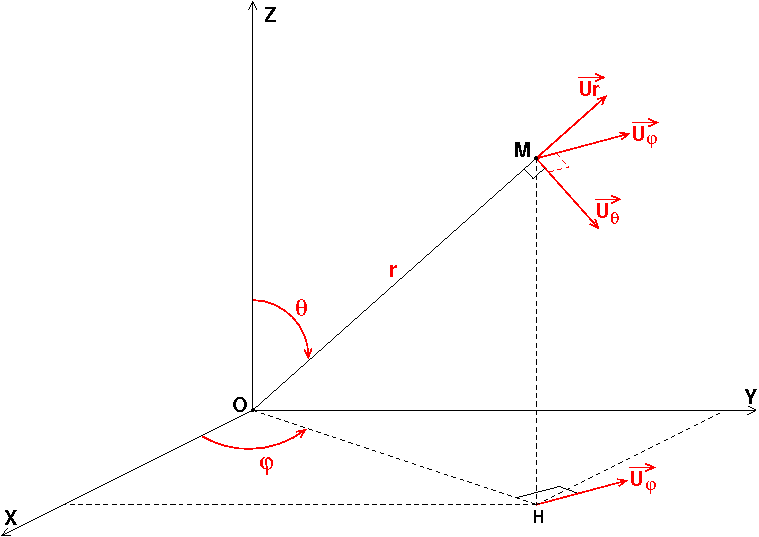
Cela dit, par simple curiosité intellectuelle, je te fournis un peu d'aide en joignant un schéma car, d'un auteur à l'autre, il y a parfois permutation de   et .
D'accord avec tes expressions des trois coordonnées. Le vecteur déplacement élémentaire a pour expression :

\overrightarrow{dl}=dr.\overrightarrow{u_{r}}+r.d\theta.\overrightarrow{u_{\theta}}+r.\sin\left(\theta\right).d\varphi.\overrightarrow{u_{\varphi}}

dr=\frac{dr}{dt}.dt=\frac{d\sqrt{a^{2}+b^{2}t^{2}}}{dt}.dt=\frac{b^{2}.t}{\sqrt{a^{2}+b^{2}t^{2}}}.dt

r.d\theta=r.\frac{d\theta}{dt}.dt=\sqrt{a^{2}+b^{2}t^{2}}.\frac{d\left(\arctan\left(\frac{a}{b.t}\right)\right)}{dt}.dt=-\frac{a.b}{\sqrt{a^{2}+b^{2}t^{2}}}.dt

r.\sin\left(\theta\right).d\varphi=r.\sin\left(\theta\right).\frac{d\varphi}{dt}.dt=a.\omega.dt

La norme du vecteur déplacement élémentaire est ainsi :

dl=\left[\frac{b^{4}.t^{2}}{a^{2}+b^{2}t^{2}}+\frac{a^{2}.b^{2}}{a^{2}+b^{2}t^{2}}+a^{2}.\omega^{2}\right].dt=\left[b^{2}.\left(\frac{a^{2}+b^{2}t^{2}}{a^{2}+b^{2}t^{2}}\right)+a^{2}.\omega^{2}\right].dt

dl=\left(b^{2}+a^{2}.\omega^{2}\right).dt

Il suffit d'intégrer sur la durée d'un tour : T=\frac{2\pi}{\omega}.

Le calcul est beaucoup plus compliqué qu'à l'aide des coordonnées cylindriques et même qu'à l'aide des coordonnées cartésiennes. Je déconseille fortement cette méthode inutilement longue et compliquée !

Mécanique du point matériel

Posté par
bissinyandoupre : Mécanique du point matériel 10-06-17 à 12:43

Excuses moi comment tu fait pour quitter de rsind/dt à awdt??

Posté par
vanoisere : Mécanique du point matériel 10-06-17 à 13:33

r.\sin\left(\theta\right)=OH=\sqrt{x^{2}+y^{2}}=a\quad;\quad\frac{d\varphi}{dt}=\frac{d\left(\omega.t\right)}{dt}=\omega
J'espère que mon message précédent t'a convaincu de la difficulté inutile de cette méthode. En revanche, le calcul en coordonnées cartésiennes est à peine plus difficile que le calcul en coordonnées cylindriques...

Posté par
bissinyandoupre : Mécanique du point matériel 10-06-17 à 13:47

Merci beaucoup Vanoise. Je suis conscient des difficultés dont tu parle. Mais désolé de te décevoir, je vais quand même essayer. J'aime trop la mécanique
Une fois de plus merci

Posté par
vanoisere : Mécanique du point matériel 10-06-17 à 13:55

Citation :
Mais désolé de te décevoir

Mais pas du tout : j'apprécie les étudiants accrocheurs qui aiment faire les choses de façon approfondie. je veux juste dire que, si tu rencontres ce type de problème un jour d'examen, choisi l'étude en coordonnées cylindriques, cartésiennes à la rigueur, mais surtout pas sphériques. Tu auras dans la suite du programme, de nombreuses occasions d'utiliser les coordonnées sphériques.

Posté par
vanoisere : Mécanique du point matériel 10-06-17 à 14:15

Je viens de me rendre compte que j'ai oublié une racine carrée dans les expressions du déplacement. Je rectifie :

dl=\left[\frac{b^{4}.t^{2}}{a^{2}+b^{2}t^{2}}+\frac{a^{2}.b^{2}}{a^{2}+b^{2}t^{2}}+a^{2}.\omega^{2}\right]^{\frac{1}{2}}.dt=\left[b^{2}.\left(\frac{a^{2}+b^{2}t^{2}}{a^{2}+b^{2}t^{2}}\right)+a^{2}.\omega^{2}\right]^{\frac{1}{2}}.dt

dl=\sqrt{\left(b^{2}+a^{2}.\omega^{2}\right)}.dt

Posté par
bissinyandoupre : Mécanique du point matériel 10-06-17 à 14:38

Ne t'inquiète pas je me suis rendu compte de l'absence de la racine carrée. Merci beaucoup


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !