Inscription / Connexion Nouveau Sujet
Mécanique du point et Théorème du moment cinétique
Bonjour,
J'ai des questions à propos de cet exercice :
Voici mes réponses :
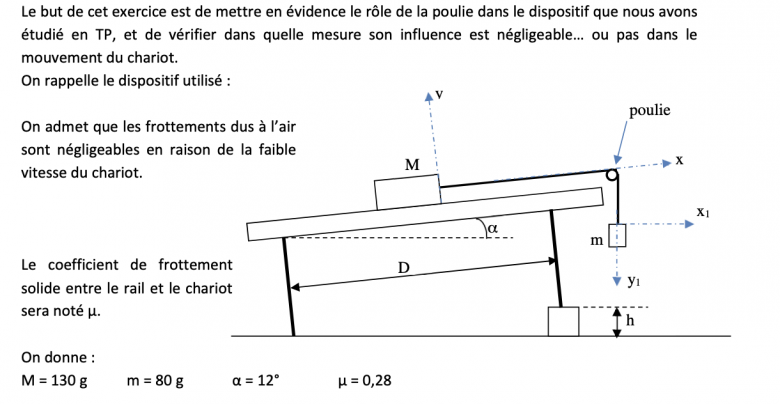
a) j'ai placé la base ex ey ez, avec ex dans la même direction que TGauche, et avec une sens opposé, ey vers le haut et ez vers nous. ex1, vers la droite, ey1 vers le bas et ez1 vers le fond.
Bilan des forces :
T gauche (vecteur) = - T gauche ex
T bas (vecteur) = + Tbas ey1
P (vecteur) = mg ey1
Réaction du support : R(vecteur) = Rx ex1 + Ry ey1
b) On ne nous précise pas dans l'exercice ce qu'est T ni T', mais je suppose que on a T gauche = T et T' = Tbas
c) Poulie à l'équilibre ==> v = 0 ==> Lo(M) = 0
Theoreme Moment cinétique appliqué ici : O = Mo (Fres) = 0
Avec Mo(P) = 0, Mo(R) = 0, Mo(T gauche) = Rp ey ^ - T ex = Rp T ez (car ey ^ ex = - ez)
De la même manière, on a
Mo(T droite) = T' Rp ez1
Ma question est la suivant : étant donné que les deux moments, s'expriment en fonction de 2 axes z, de sens opposés, as on le droit de dire que on a alors Mo( T gauche) = - Rp T ez1
Auquel cas, on aurait, en projection sur ez1 : 0 = T' Rp - T RP <==> T' = T
Merci pour votre aide,

POur la d) :
i) on a Lo(M) = Jw avec w la vitesse angulaire et J le moment d'inertie
ii)Mo( T gauche ) = RpT ez et Mo(T bas) = TpT' ez1
donc en partant de mon hypothèse de tout à l'heure :
Mo (T bas) = -T'Tp ez
iii) TMC selon ez : J.(dw/dt) = RpT = RpT'
==> 1/2 mp Rp^2 (d^2 téta/dt^2) = Rp(T-T')
En réarrangeant l'expression, on a
d^2 téta / dt^2 = 2 (T-T') / mp
Je pense que j'ai faux car je ne vois pas l'interêt de nous faire recopier les moments déjà exprimé à la question c)
Bonjour,
Pour le début on a bien T'=T ... à condition de définir T et T'.
Je suppose que Tp=Rp ?
Je suppose que T et T' ont été définies dans 1 et qu'il s'agit de l'action du fil sur M et m ?
Sinon c) et d)ii) c'est bien la même chose.
Pour iii) il y a manifestement un Rp de disparu, un = qui est un - ....
Utilisez au minimum les exposants (bouton x2) ou mieux le bouton LTX.
d^2 téta / dt^2 écrit \frac{d^2\theta}{dt^2} donne
\dfrac{d^2\theta}{dt^2[tex] ce qui est plus lisible.
Merci pour votre réponse.
Oui, Tp = Rp (erreur de frappe !)
Je réécris le iii) Avec ltx pour que ce soit plus clair.
TMC selon ez : J = RpT - RpT'
==> 1/2 mp Rp^2 = Rp(T-T')
En réarrangeant l'expression, on a
Pour ce qui est de ce que j'ai fait pour la c), ai-je bien le droit de dire que ez = -ez1 ?


