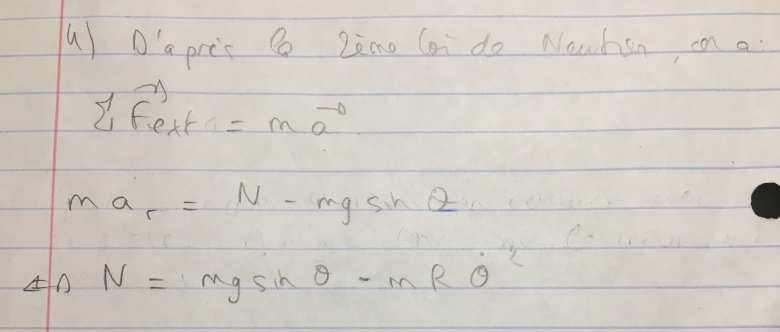Inscription / Connexion Nouveau Sujet
Mécanique du point base polaire portion de cercle
Bonjour,
On me propose l'énoncé suivant:
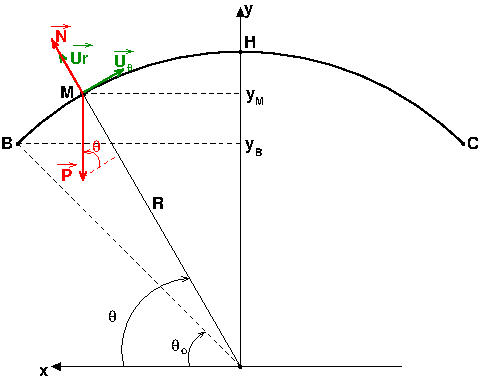
"Entre B et C, la piste est une portion de cercle de rayon R et de centre O". On néglige
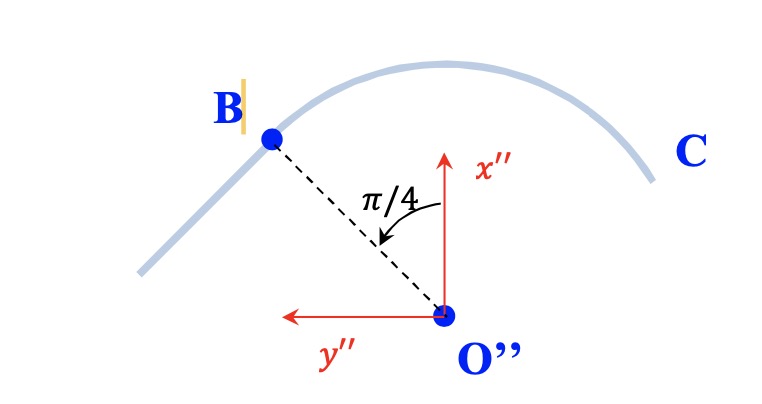
les frottements et on suppose que M reste en contact avec la piste. On note Vb la vitesse de M lorsqu'il passe en B. On notera r et  les coordonnées polaires de M avec 0"x" l'axe polaire.
les coordonnées polaires de M avec 0"x" l'axe polaire.
On étudie le mouvement de M dans le repère mobile (M, Ur, U ).
).
1.Faire un schéma pour une position quelconque de M sur la portion BC et représenter l'angle  ainsi que les vecteurs Ur et U
ainsi que les vecteurs Ur et U ".
".
Bonsoir
Certaines formules sont illisibles et quelles sont les questions ?
Qu'as-tu réussi à faire et qu'est-ce qui te bloque ?
Si la figure n'est pas imposée, il y a sans doute moyen de faire plus simple. N'ayant pas toutes les questions, je dois me contenter de généralités : il faut choisir les orientations de façons à devoir ensuite manipuler autant que possibles des valeurs positives et avoir des conditions initiales les plus simples possibles.
Fournir l'intégralité de l'énoncé permet de mieux guider l'étudiant vers la méthode la plus efficace.
Mes excuses, je pensais avoir inclut l'ensembles des questions (j'ai dû faire un mauvais copier coller).
Voilà l'entièreté des questions:
" 1) Faire un schéma pour une position quelconque de M sur la portion BC et représenter l'angle  ainsi que les vecteurs Ur et U
ainsi que les vecteurs Ur et U
2) Donner l'expression de la vitesse de M dans la base (Ur, U ) et en déduire l'expression de son accélération.
) et en déduire l'expression de son accélération.
3) Donner l'expression des forces exercées sur M dans cette base.
4) En utilisant la 2e loi de Newton, écrire les équations du mouvement de M.
5) Retrouver l'une de ces équations en utilisant le théorème du moment cinétique.
6) Donner l'expression du vecteur déplacement dr et en déduire le travail effectué sur
M au cours d'un déplacement infinitésimal dr.
7) Donner l'expression du travail effectué entre le point B et le sommet de la piste.
8) En déduire la vitesse de M au sommet de la piste.
9) À quelle condition sur le point M va t-il quitter la piste lorsqu'il passe à son sommet ?"
La figure est imposée à la question 1. J'ai du mal à déterminer où se trouve l'angle  dans ce cas-là notamment à cause du fait que l'on est sur une portion de cercle et non un cercle.
dans ce cas-là notamment à cause du fait que l'on est sur une portion de cercle et non un cercle.
Le choix de ton schéma de 19h00 est tout à fait possible. Il a l'avantage de faire intervenir une vitesse angulaire positive.
Qu'as-tu réussi à faire ensuite ? Qu'est-ce qui te bloque exactement ?
Poser ces questions permet d'aider plus efficacement en tenant compte du niveau de l'étudiant...
Il manque une information dans la question 9, elle doit se lire:
"À quelle condition sur *Vb* le point M va t-il quitter la piste lorsqu'il passe à son sommet ?"
Je m'excuse d'avance, ce que je vais écrire est très loin d'être rigoureux mais cela permet d'exprimer ce qui me bloque:
Dans mon schéma de 19h00, ce qui me fait hésiter c'est que l'angle entre l'axe y'' et B n'est pas "dans un cercle" alors que l'angle entre B et M est dans la portion de cercle. Mon angle  a donc "une partie" qui n'est pas dans la portion de cercle. Je voulais savoir si cela est problématique.
a donc "une partie" qui n'est pas dans la portion de cercle. Je voulais savoir si cela est problématique.
Sur le schéma suivant:
Faudrait-il que je choisisse l'angle  1 ou l'angle
1 ou l'angle  2 comme mon angle
2 comme mon angle  sur mon schéma final ?
sur mon schéma final ?
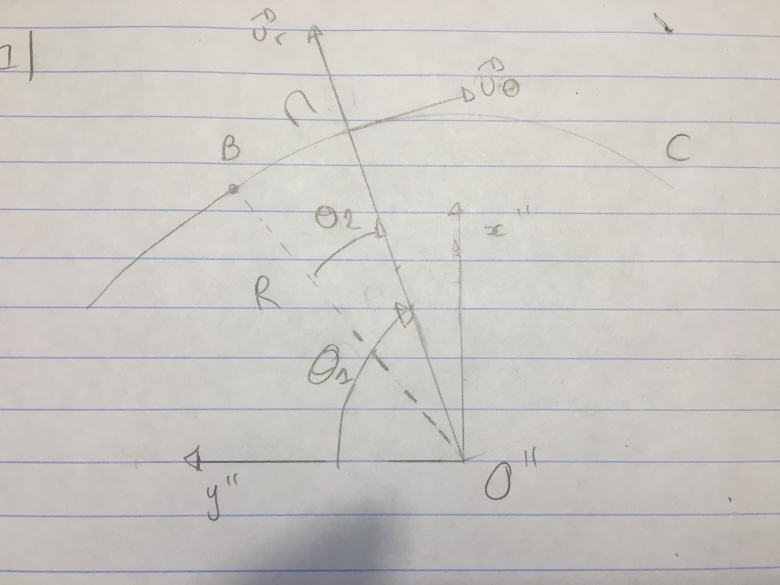
Ton choix ne pose pas de problème : il suffit de considérer :
 >
>  o
o
avec
 o=(
o=( /4) rad
/4) radC'est à inclure avant le schéma dans ma rédaction ou c'est uniquement pour mieux comprendre ? ^^
J'ai l'impression en lisant vos réponses qu'il y a plusieurs choix possible pour
 , cela veut-il dire que je pourrais aussi utiliser l'angle
, cela veut-il dire que je pourrais aussi utiliser l'angle  2 qui est sur mon schéma de 19h20 pour mon angle
2 qui est sur mon schéma de 19h20 pour mon angle  (au lieu d'utiliser l'angle
(au lieu d'utiliser l'angle  1) ? Ou serait-il incorrect d'utiliser l'angle
1) ? Ou serait-il incorrect d'utiliser l'angle  2?
2? Avec ton premier choix,  change de signe au sommet de la trajectoire...
change de signe au sommet de la trajectoire...
Fais le choix qui te paraît le plus simple.
Etant donné que je dois considérer le sommet de la trajectoire dans les questions suivantes, je suppose que mon premier choix est le plus judicieux. Merci pour votre aide.
Je vais attaquer les questions suivantes et je posterai une réponse si je bloque quelque part 
Bonsoir,
J'ai avancé dans mon exercice:
Pour les projections, j'ai utilisé mon premier schéma, celui que j'ai envoyé à 19h00.
Serait-il possible de savoir si cela est correct?
(je n'ai pas inclut la rédaction pour éviter d'avoir des images trop grandes ^^)
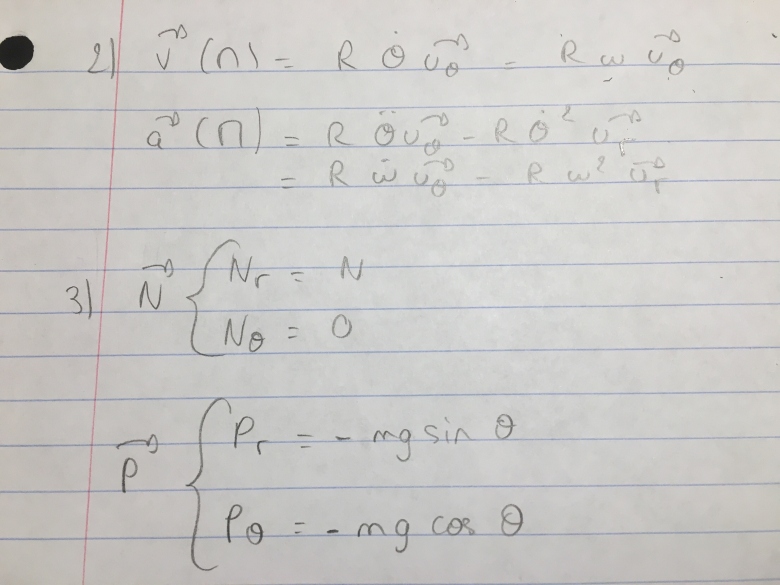
Aussi, je bloque un peu sur la question 4 pour trouver les équations du mouvement de M.
Voici ce que j'ai fais, je ne sais pas je suis sur la bonne voie:
J'ai fait la question 5 qui demande de retrouver une des équations du mouvement à l'aide du théorème de l'énergie cinétique et j'ai retrouvé l'expression que j'avais trouvé pour la question 4.
Est-ce bien la bonne expression?
Pour la question 6, j'ai écrit:
dr = dl Ur (avec dl la distance parcourue par M entre t et t + dt)
J'ai dit que le travail de N est nul car N est constamment perpendiculaire au déplacement infinitésimal dr.
Donc, pour le travail effectué sur M au cours d'un déplacement infinitésimal, on a:
dW = P . dl Ur = -mgsin dl
dl
Suis-je sur la bonne voie?
Pour la question 7, je pense qu'il faut déterminer la distance entre le point B et le sommet de la piste mais je ne vois pas comment je pourrais obtenir cela...
Auriez-vous des pistes?
Pour la projection du poids : tout dépend de la convention d'orientation de l'angle  et de la définition de cet angle. Peux-tu fournir un dernier schéma précisant la convention que tu as finalement adoptée ?
et de la définition de cet angle. Peux-tu fournir un dernier schéma précisant la convention que tu as finalement adoptée ?
La méthode d'obtention de l'équation différentielle vérifiée par  est bonne. Cette équation n'admet pas de solution exacte mais une telle résolution n'est pas demandée :
est bonne. Cette équation n'admet pas de solution exacte mais une telle résolution n'est pas demandée :
Pour le théorème de l'énergie potentielle : effectivement, seul le poids travaille. Ta méthode est correcte sachant que le déplacement élémentaire peut s'écrire :
dl=R.d
Tu peux aller un peu plus vite en utilisant l'expression générale du travail du poids en fonction de m.g et de la variation d'altitude entre B et M que tu peux facilement exprimer en fonction de R et  .
.
Bonjour,
Merci pour votre réponse.
J'attache le schéma que j'ai utilisé pour mes projections de forces.
Serait-il possible de savoir si, en considérant ce schéma, mes projections sont correctes?
Concernant le déplacement élémentaire, comment avez-vous déduit que dl = R . d ? (d'ailleurs, est-ce que c'est un produit scalaire ou une multiplication? ^^).
? (d'ailleurs, est-ce que c'est un produit scalaire ou une multiplication? ^^).
Tu peux aller un peu plus vite en utilisant l'expression générale du travail du poids en fonction de m.g et de la variation d'altitude entre B et M que tu peux facilement exprimer en fonction de R et
 .
.Je dois appliquer cela pour la question 6 et 7 ?
Serait-il possible de savoir si, en considérant ce schéma, mes projections sont correctes?
Oui !
Concernant le déplacement élémentaire, comment avez-vous déduit que dl = R . d
 ?
?Le vecteur déplacement élémentaire, pour une trajectoire circulaire de rayon R s'écrit :
Cela résulte de la définition du radian (voir ici si nécessaire :
Je dois appliquer cela pour la question 6 et 7 ?
Oui !
Je vous avoue que je bloque un peu sur la variation d'altitude.
Je ne sais pas si cela est judicieux mais je pourrais intégrer mon expression du travail infinitésimal de  /4 à
/4 à  /2 ?
/2 ?
Étant donné que, lorsque, M arrive au sommet de la piste on a  =
=  /2.
/2.
Au somme de la trajectoire, on a  =
=  /2
/2
Donc pour le travail effectué entre le point B et le sommet on a:
W = -mg(sin( /2) - sin(
/2) - sin( /4))
/4))
En remplaçant on a donc:
W = -mg(1 - sqrt(2)/2) = -mg((2 - sqrt(2))/2)
Est-ce bien cela?
avec :
D'ailleurs, ne manque-t-il pas un R ici ? Car dans ce message:
Tu peux aller un peu plus vite en utilisant l'expression générale du travail du poids en fonction de m.g et de la variation d'altitude entre B et M que tu peux facilement exprimer en fonction de R et
 .
.Vous m'aviez conseillé d'exprimer la variation d'altitude (yM-yB) en fonction de R et
 .
. Oui. Pour la suite, il faut connaître la vitesse initiale Vo en B.
Tu peux finir le problème puis revenir à la question 5 où on demande de retrouver l'équation différentielle à partir du théorème de l'énergie cinétique.
J'ai aussi essayé d'intégrer l'expression du travail sur une distance infinitésimal pour vérifier le résultat que j'ai obtenue en passant par l'énergie potentielle. Cependant, j'obtiens un résultat différent.
Sauriez-vous d'où vient le problème?
Peut-être que, finalement, la relation correct était celle-ci ?
Ce n'est clairement pas ça car, comme vous m'avez indiqué, y = Rsin(
 )
) J'avais effectivement oublié le R dans l'expression du travail du poids. On obtient :
On obtient le même résultat (heureusement !) en partant du travail élémentaire :
Ah mais oui c'est l'expression de mon déplacement élémentaire qui est incorrect, j'avais pris Ur comme vecteur tangent à la trajectoire alors que c'est U . Du coup je me suis retrouvé avec du sin
. Du coup je me suis retrouvé avec du sin  à intégrer au lieu du cos
à intégrer au lieu du cos .
.
Je vais rédiger tout cela sur mon brouillon et attaquer les 2 dernières questions. Je reporterai un message d'ici peu 
Voilà ce que j'ai écrit pour la question 8:
On note S le sommet de la trajectoire.
D'après le théorème de l'énergie cinétique, on a:
 Ec = Ec(S) - Ec(B) = WB
Ec = Ec(S) - Ec(B) = WB S
S
Ec(S) = 1/2mVs^2, Ec(B) = 1/2mVb^2, WB S = -mgR((2-sqrt(2))/2)
S = -mgR((2-sqrt(2))/2)
On a donc:
1/2mVs^2 - 1/2mVb^2 = -mgR((2-sqrt(2))/2)
1/2Vs^2 = 1/2Vb^2 - gR((2-sqrt(2))/2)
Vs^2 = Vb^2 - 2gR((2-sqrt(2))/2)
Vs = sqrt(Vb^2 - 2gR((2-sqrt(2))/2))
Est-ce bien cela?
Concernant la question 9, j'ai une idée de l'information que l'on peut utiliser mais je suis pas sûr:
Pour que M quitte la piste, il faut que la réaction N s'annule.
Cependant, je ne vois pas vraiment comment utiliser cette information et le fait qu'on veut que M décolle à  =
=  /2 pour trouver la condition sur Vb.
/2 pour trouver la condition sur Vb.
Dans le cas particulier du sommet, tu peux projeter la relation fondamentale de la dynamique suivant la verticale. Cela va te permettre d'obtenir N. Pour conclure, comme tu l'as écrit, il faut N>0 pour que le contact avec la piste persiste.
Que voulez-vous dire par projeter suivant la verticale? Je devrais projeter selon mon axe y comme ceci?
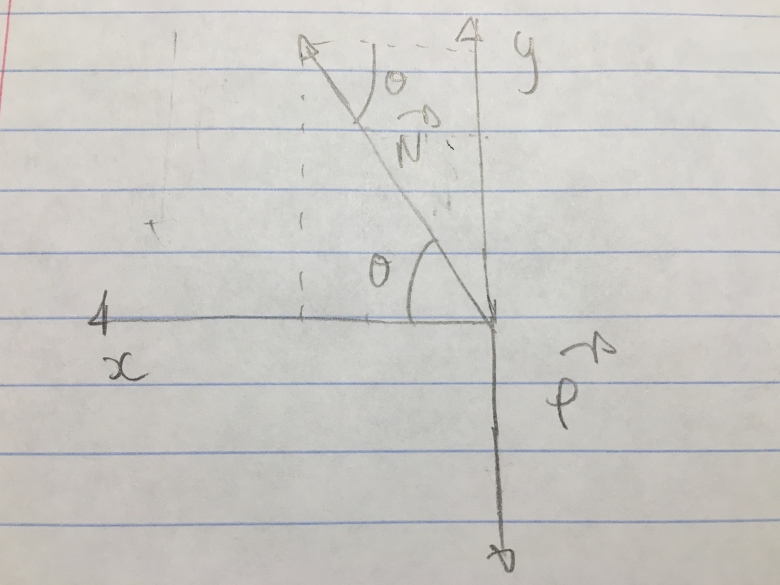
Si je comprends bien, ce que je dois faire c'est:
J'ai N = mgsin - mR
- mR '^2
'^2
Du coup je dois trouver l'expression de la vitesse angulaire et remplacer dans N, puis je remplace  dans N par
dans N par  /2 et je détermine l'expression de Vb.
/2 et je détermine l'expression de Vb.
Je crois que j'ai fait une erreur ici:
Au lieu de:
mar = N - mgsin
je devrais avoir:
-mar = N - mgsin
car l'accélération centripète est dirigé dans le sens inverse du vecteur Ur
Est-ce correct?
J'ai fait le raisonnement pour la question 9 et je trouve Vb = 7.27 m/s
J'ai l'impression que cela est beaucoup trop élevé. Voici ma rédaction, pourriez-vous m'indiquer si j'ai fait une erreur ?