Ton message de 18h25 : il y a une simplification par 2 :



Dans le cas particulier du sommet :



M quitte la piste si la valeur théorique de N devient négative :



Étourderie dans ta dernière ligne ; sinon : tu as bien travaillé !

Reste la question 5 où il suffit de dériver par rapport au temps l'expression obtenue par application du théorème de l'énergie cinétique entre B et M.

Merci beaucoup pour votre aide.

Pour la question 5, j'ai appliqué le théorème du moment cinétique qui m'a permis de retrouver l'équation du mouvement que j'ai trouvé dans la question 4.

Faut-il que je fasse quelque chose en plus? J'ai l'impression que la question 5 ne demande pas plus ^^

Jawad0610 @ 02-03-2020 à 19:08

Mes excuses, je pensais avoir inclut l'ensembles des questions (j'ai dû faire un mauvais copier coller).

Voilà l'entièreté des questions:

" 1) Faire un schéma pour une position quelconque de M sur la portion BC et représenter l'angle 􏰝 ainsi que les vecteurs Ur et U

2) Donner l'expression de la vitesse de M dans la base (Ur, U) et en déduire 􏰟􏰠l'expression de son accélération.

3) Donner l'expression des forces exercées sur M dans cette base.

4) En utilisant la 2e loi de Newton, écrire les équations du mouvement de M.

5) Retrouver l'une de ces équations en utilisant le théorème du moment cinétique.

6) Donner l'expression du vecteur déplacement dr et en déduire le travail effectué sur
M au cours d'un déplacement infinitésimal dr.

7) Donner l'expression du travail effectué entre le point B et le sommet de la piste.

8) En déduire la vitesse de M au sommet de la piste.

9) À quelle condition sur 􏰁􏰜 le point M va t-il quitter la piste lorsqu'il passe à son sommet ?"

Parfait ! Tu as bien travaillé !

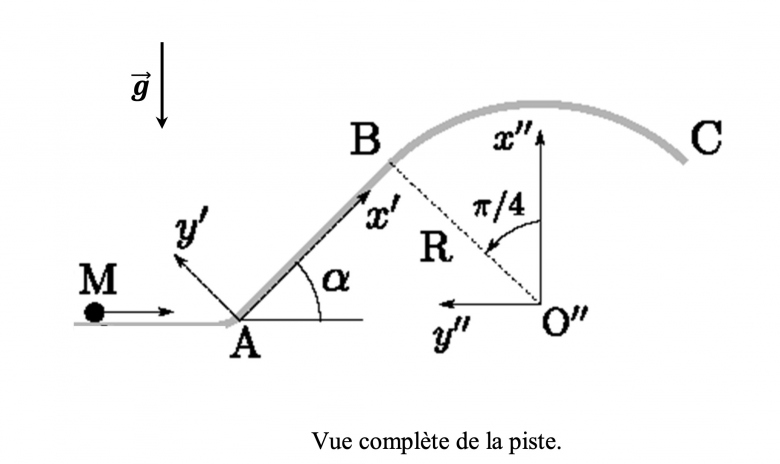
Aussi, cette exercice fait partie d'un problème plus générale schématisé sur l'image attaché ci-dessous.

Il y a trois parties au problème presque indépendantes les unes des autres:

1) Le glissement de M entre A et B

2) Le glissement de M entre B et C

3) La phase de propulsion de M (par un ressort)

Le problème consiste à déterminer la valeur minimale de Va pour que M quitte la 􏰂
piste lorsqu'il parvient au sommet de la courbe BC.

Dans cette discussion, nous avons considéré la 2ème partie.

J'ai déjà bien avancé sur la 1ère et 3ème partie mais je ne suis pas toujours certain de ce que j'écris ^^.

Serait-il possible pour moi de poster les deux autres parties dans deux autres sujets différents?

J'ai oublié d'attacher le schéma

Sans vouloir me précipiter, je vais tout de même créer un sujet pour la première partie du problème.

Bonsoir,

@Jawad0610 : ne pas abuser des insertions d'image pour du texte, tu as tout ce qu'il faut pour faire autrement :

extrait de la FAQ du forum :

Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?

Oui, cela est même encouragé.

Les correcteurs sont généralement plus attirés par un message bien écrit en Latex et bien présenté que par un message écrit avec les caractères normaux, non aéré, etc.

Le Latex est un outil mathématique qui pouvait nous permettre à tous de faciliter la lecture et la compréhension en écrivant proprement nos formules mathématiques. Nous vous invitons à prendre connaissance du guide latex présent sur le site. Un tutorial complet vous aide à faire vos premiers pas.
Bien-sûr, l'utilisation du Latex n'est pas obligatoire, mais pourquoi se priver d'un tel outil ?

Si ce langage vous semble trop compliqué à utiliser dans un premier temps, il vous est cependant possible d'insérer très simplement des caractères mathématiques dans votre texte en utilisant l'outil présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le mode d'emploi du forum.