Inscription / Connexion Nouveau Sujet
Mécanique du point
Bonjour à tous,
Je rencontre quelques problèmes pour résoudre un exercice.
SUJET
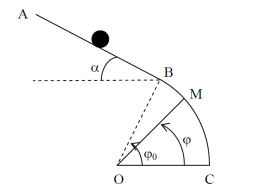
Une glissière est constituée d'une partie rectiligne AB et d'un arc de cercle BC de centre O et de rayon a. (l'arc est dans le prolongement du plan incliné) Un solide ponctuel est lâché du point A sans vitesse initiale. Les frottements sont négligeables.
1) En appliquant le théorème de l'énergie cinétique exprimer la vitesse v au point M repéré par ses coordonnées polaires (a, ).
2) Appliquer le principe fondamental de la dynamique et déterminer l'expression de la
réaction R exercée par la glissière sur le mobile au point M.
3) Montrer que le mobile quitte la glissière en un point D de coordonnées (a, ).
4) Calculer alors la valeur numérique de ainsi que le module de la vitesse du mobile en D.
Données numériques : AB = 1 m, a = 2 m,= 60°,
= 30°, g = 9,81 m.s-2
Vous trouverez une image de la figure ci-dessous.
MES RÉPONSES
1) D'après le T.E.C,
Après de nombreuses tentatives, je n'ai pu calculer le travail en utilisant le repère de Frenet, je crois que tout bloque ici.
2) D'après le PFD .
Dans le repère de Frenet on a :
D'où :
3) et 4) J'ai l'idée d'utiliser le fait que le mobile est en contact tant que Rn > 0, donc de résoudre l'inéquation, mais sans le travail impossible de tenter cette approche.
Je crois donc que tout vient du travail, mais le reste du raisonnement me paraît incomplet. C'est pourquoi je demande votre aide pour m'aiguiller vers les bonnes réponses.
Merci de prendre du temps pour moi,
Lantean
Bonjour
Il te faut déterminer la variation d'altitude entre A et B puis entre B et M. Un peu de trigonométrie... Je te laisse réfléchir.
Pour la question 2 : tu peux exprimer les composantes normale et tangentielle de l'accélération ? Attention à ne pas confondre l'accélération et la distance a= OM.
Donc sans utiliser le théorème de l'énergie cinétique ?
Bien sûr que si mais l'expression du travail du poids fait intervenir la dénivellation entre le point A et le point M ; d'où l'intérêt de mon message de 18h25.
Bonjour,
J'ai pu déduire de l'expression du travail que .
Donc, en injectant dans l'inéquation Rn>0, je trouve (après les calculs) que :
Mais application numérique faite, j'obtiens environ 82°C.
J'ai également exprimé l'accélération tangentielle mais R n'ayant pas de composantes tangentielle je ne sais pas quoi en faire.
Cela dit vos réponses m'ont permis de faire de net progrès, merci à vous
Il faut réfléchir au réalisme des résultats : la valeur de 
correspondant au point M où le solide quitte la glissière est nécessairement inférieure à 60° ! De plus, il ne s'agit pas de degrés Celsius !
1° : Quelle est l'expression de (zA - zM) ?
2° : Quelle est l'expression de l'accélération normale de M sur la partie circulaire de la trajectoire ?
3° : Quelle est l'expression de RN ?
Après avoir répondu à ces questions, tu pourras déterminer la valeur de lorsque M quitte la glissière
J'ai également exprimé l'accélération tangentielle mais R n'ayant pas de composantes tangentielle je ne sais pas quoi en faire.
Cette expression ne semble pas demandée. Elle n'est pas nulle dans la mesure où le poids possède une composante tangentielle.
Degré Celsius 
j'ai peu dormi...
D'après mes calculs
(a étant l'inverse du rayon de courbure)
Je ne vois pas mon erreur, mais je suis persuadé que c'est tout bête...
Non :
Formule à revoir en tenant compte de la correction précédente. Attention aussi aux signes...
En prenant en compte vos corrections, je trouve un angle de 24° environ.
Effectivement la masse n'apparaît pas, mais il ne s'agissait que d'une erreur de recopiage.
Par contre je croyais que dans l'expression de l'accélération normale, c'est à dire , r était égal au rayon de courbure. Qu'en pensez-vous ?
L'expression de la réaction devrait maintenant être :
J'ai un petit doute sur le signe du second membre mais ça fait une solution dans les complexes si je mets un + donc nouvelle interrogation de ma part.
Merci de votre aide, je crois qu'on y est presque 
Par contre je croyais que dans l'expression de l'accélération normale, c'est à dire
C'est bien cela avec ici : r= a (distance OM : utiliser la même lettre pour désigner l'accélération et le rayon de courbure n'est pas une très bonne idée...)
Tu as un problème de signe. Tu peux éventuellement poster un scan de la figure où tu auras représenté les différents vecteurs ?
C'est bien cela avec ici : r= a (distance OM : utiliser la même lettre pour désigner l'accélération et le rayon de courbure n'est pas une très bonne idée...)
Je vous le fais pas dire, mais OM est le rayon et pas le rayon de courbure, c'est de là que vient mon interrogation.
Tu as un problème de signe. Tu peux éventuellement poster un scan de la figure où tu auras représenté les différents vecteurs ?
Je sais pas si c'est très net mais voilà. Autre chose : je n'utilise à aucun moment g. Je pense néanmoins que l'angle ne dépend pas de g.
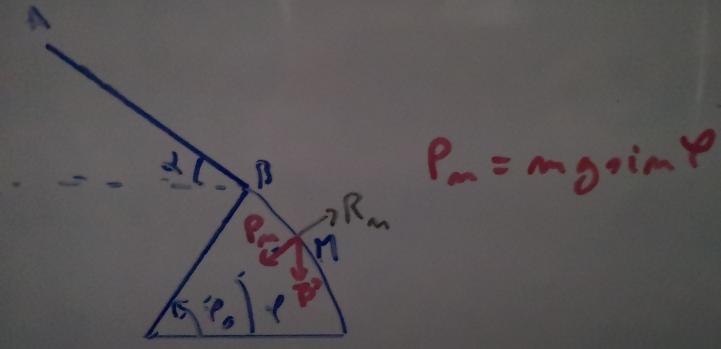
Le vecteur accélération normale est orienté vers le centre comme le vecteur unitaire.
Accélération tangentielle est orienté de manière orthonormale au vecteur accélération normale "vers la droite".
Je sens que vous essayez de me faire voir quelque chose mais je dois être aveugle
Projete la relation fondamentale de la dynamique sur un axe orienté de M vers O.
Dans le cas d'un mouvement circulaire, rayon de courbure et rayon de la trajectoire sont deux valeurs égales.
Effectivement je voyais pas les choses sous cet angle.
Mais je n'arrive pas à résoudre mon problème de signe, je ne vois pas d'où il vient..
En projetant sur un axe orienté de M vers O, sachant que l'accélération normale est centripète :
Car la réaction de la glissière est centrifuge. Donc :
Il y avait bien un problème de signe dans tes messages précédents.
Annuler
connectez vous