Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie SupérieurOn parle exclusivement de physique/chimie, pour le supérieur principalement, les BTS, IUT, prépas... LicenceForum Supérieur de licence PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau licence
Partager :

Mécanique du point

Posté par
azer44170 23-12-19 à 12:47

Bonjour,
Je me suis déjà occupé des questions sur le tremplin. Je suis rendu à cette question (sur la rampe) :
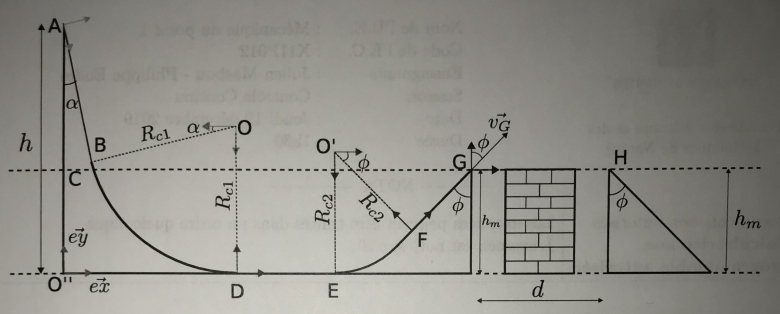
Déterminer la vitesse au point B, vB, pour un skateur partant du point A avec une vitesse initiale nulle. Exprimer vB en fonction de h, RC1, g et alpha. J'ai trouvé :
v_B=\sqrt {\frac {2g.AB}{\cos(\alpha )}}
Cependant j'imagine qu'il faut que j'exprime AB en fonction de RC1 et h. Je n'ai toutefois aucune idée de comment faire.

Mécanique du point

Posté par
vanoisere : Mécanique du point 23-12-19 à 14:43

Bonjour
En appliquant le théorème de l'énergie cinétique  : le travail du poids s'exprime directement en fonction de h.

Posté par
azer44170re : Mécanique du point 23-12-19 à 15:23

Le problème est que nous n'avons pas vu les énergies (cinétique, mécanique...). Nous avons vu que la cinématique et la dynamique newtonienne avec les trois lois de Newton 😅

Posté par
azer44170re : Mécanique du point 23-12-19 à 15:37

Désolé pour ces nombreuses images.

Mécanique du point

Posté par
vanoisere : Mécanique du point 23-12-19 à 18:53

\frac{AB}{\cos\left(\alpha\right)} représente la distance AB' où B' est le projeté orthogonal de B sur la verticale O"A.
La distance O"B' peut s'exprimer en fonction de Rc1 et de \cos\left(\alpha\right).

Posté par
azer44170re : Mécanique du point 23-12-19 à 19:53

Merci. Donc :
AB'=\frac {AB}{\cos(\alpha )}
O''B'=h-AB'
O''B'=h-\frac {AB}{\cos(\alpha )}
Je ne vois pas comment exprimez O"B' en fonction de RC1 et \alpha comme vous dites.

Posté par
vanoisere : Mécanique du point 23-12-19 à 21:29

Soit O' le projeté orthogonal du centre O sur la verticale O”A.

O”B'=O”O'-O'B' avec :

O''O'=R_{c1}\quad;\quad O'B'=R_{c1}.\sin\left(\alpha\right)

O''B'=R_{c1}.\left[1-\sin\left(\alpha\right)\right]

Posté par
azer44170re : Mécanique du point 23-12-19 à 21:39

Merci beaucoup, je n'y aurais jamais pensé !


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !