Inscription / Connexion Nouveau Sujet
Mécanique du Point
Bonjour, j'aurais besoin de votre aide concernant certaines question d'un exercice que je n'arrive pas à faire.
Le référentiel ℜ, considéré comme galiléen, est rapporté au repère (O, x, y, z).
Un mobile P, de masse m, considéré comme ponctuel, est lâché avec une vitesse initiale v0 d'une hauteur z0 . Il est astreint à glisser sans frottement sur une hélice d'équations :
x = R cos θ
y = R sin θ
z = h θ
où R et h sont respectivement le rayon et le pas apparent de l'hélice.
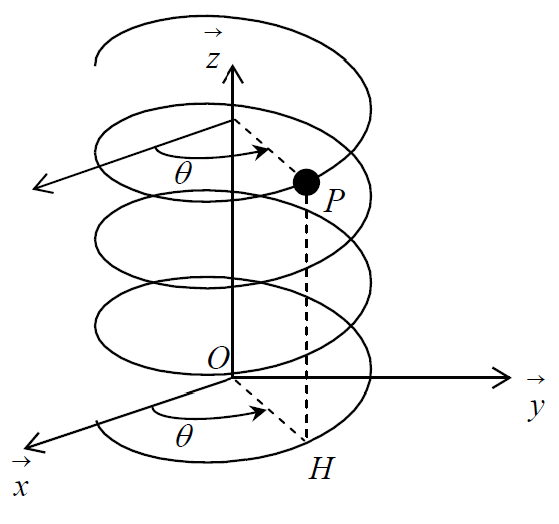
La position du mobile P est repérée grâce à l'angle θ défini dans le plan xOy par θ = (Ox, OH), où H est la projection orthogonale de P dans le plan xOy.
On note g = − gz l'accélération de la pesanteur.
1.1 Exprimer dans ℜ la vitesse vP du mobile P.
1.2 Exprimer dans ℜ l'accélération aP du mobile P.
1.3 Réaliser le bilan des actions mécaniques extérieures appliquées au mobile P.
1.4 Énoncer le principe fondamental de la dynamique appliqué au mobile P.
1.5 En déduire l'équation du mouvement.
1.6 Déterminer la loi d'évolution θ(t) donnant l'angle θ en fonction du temps t, de v0 et z0.
1.7 En déduire les composantes de la force de liaison entre le mobile P et l'hélice.
Réponses :
1.1 On a :
OP = x + y + z
Ainsi :
vP = d(OP) / dt = θ'(R*eθ + h*z)
1.2
aP = d(vP) / dt = θ''(R*eθ + h*z) - θ2'*R*z
1.3
Bilan des Forces :
P = mg
1.4
Principe Fondamental de la Dynamique appliqué au point P :
 fext. P = m*aP
fext. P = m*aP
1.5
Après "calculs" j'arrive à une équation différentielle :
Je que pense qu'ici j'ai faux...
1.6
Il faut surement résoudre l'équation différentiel.
1.7
Qu'est-ce donc une force de liaison ?
Merci.
salut
je pense que tu as la bonne expression de l'accélération même si ce n'est pas tout à fait bien écrit ^^
ton gros problème c'est que tu oublies juste la force de liaison dans le PFD ! La force de liaison c'est tout simplement la réaction du support sur le mobile
Je souhaite revenir sur cette exercice :
1) vp = -R*θ*sin(θ) x + R*θ*cos(θ) y + h*θ' z
2) ap = -R(θ'*sin(θ) + θ*cos(θ)) x + R(θ'*cos(θ) - θ*sin(θ)) y + h*θ" z
3) - Poids du mobile P : P = -mg*z
- Réaction du support (l'Hélice) R sur le mobile P : R = R*z
4) P.F.D. appliqué au mobile P :
m*a = P + R -> m*a = -mg*z + R*z
5) m*a = -mg*z + R*z sur (Oz) donne : m*a = -mg + R
-> z(t) = 1/2 (R/m - g) t² + vO t + zO
6) z(t) = h*θ(t) = 1/2 (R/m - g) t² + vO t + zO
-> θ(t) = 1/2 (R/(mh) - g/h) t² + vO/h t + zO/h
7)...
Le début est correcte ?
bonsoir,
un an après tu reprends l'exo! 
1) vp = -R*θ'*sin(θ) x + R*θ'*cos(θ) y + h*θ' z
2)non, tu as mal dérivé vp
3) R = R z
non
il faudra utiliser le repère tournant (comme tu avais commencé l'an passé 
sinon ça va être difficile
sauf erreur
1) vp = -R*θ'*sin(θ) x + R*θ'*cos(θ) y + h*θ' z
2) ap = -R(θ"*sin(θ) + θ'²*cos(θ)) x + R(θ"*cos(θ) - θ'²*sin(θ)) y + h*θ" z
J'avais oublié les dérivées de θ(t) dès le calcul de la vitesse...
1.3 Réaliser le bilan des actions mécaniques extérieures appliquées au mobile P.
P (poids) et R (réaction du support ou encore "force de liaison")
R est normale à la trajectoire puisqu'on néglige les frottements
1.4 Énoncer le principe fondamental de la dynamique appliqué au mobile P.
ma = P + R
1.5 En déduire l'équation du mouvement.
c'est là que je suis surpris qu'on ne te dise pa d'utiliser un repère tournant. As-tu recopié tout l'énoncé?
Bon j'ai mis R sous trois composantes Rx, Ry et Rz.
L'équation du mouvement donne :
x(t) = 1/2 (Rx/m) t² + vOxt + xO
y(t) = 1/2 (Ry/m) t² + vOyt + yO
z(t) = 1/2 (Rz/m - g) t² + vOzt + zO
Or :
x(t) = r cos θ(t)
y(t) = r sin θ(t)
z(t) = r θ(t)
Ça nous fais :
θ(t) = cos-1(1/2 (Rx/mr) t² + (vOx/r)t + xO/r)
= sin-1(1/2 (Rx/mr) t² + (vOx/r)t + xO/r)
= 1/2 (Rz/mh - gh) t² + (vOz/h)t + zO/h
Pour connaitre R, je fais passer tout de l'autre côté excepté Rx, Ry et Rz...
Mais ils vont dépendre du temps...
Sinon je ne vois pas ce que ça va faire d'utiliser un repère cylindrique ou sphérique...
Je laisse le lien de l'exercice : http://ccp.scei-concours.fr/deug/sujet/2011/deug_meca1.pdf
L'équation du mouvement donne :
x(t) = 1/2 (Rx/m) t² + vOxt + xO
[...]
ah bon? je sais qu'il est tard mais ces équations sont assez surprenantes.

comment trouves-tu ça ?
|ax |0 |Rx
m |ay = -m|0 + |Ry
|az |g |Rz
|ax |0 |Rx
|ay = - |0 + 1/m |Ry
|az |g |Rz
En intégrant...
|vx |vOx |0 |Rx
|vy - |vOy = - t|0 + t/m |Ry
|vz |vOz |g |Rz
On continue... Et :
x(t) = 1/2 (Rx/m) t² + vOxt + xO
y(t) = 1/2 (Ry/m) t² + vOyt + yO
z(t) = 1/2 (Rz/m - g) t² + vOzt + zO
c'est bien ce que je craignais.
attention!
R dépend du temps a priori, donc Rx= Rx(t), Ry=Ry(t) Rz=Rz(t)
tu n'as pas le droit de supposer que ce sont des constantes lorsque tu intègres (il faudrait le démontrer et ici ça m'étonnerait que R soit constante )
mais bon, oublie (O,x,y,z) il faut prendre un autre repère pour faire l'étude à mon avis
J'ai fais comme vous me l'aviez dit :
Rx = -m*R*θ'²
Ry = m*R*θ"
Rz = m(R*θ" + g)
Mais pour l'équation du mouvement demandé dans la question précédente (1.5) je ne la mets pas vu R dépend du temps je devrais mettre des doubles intégrales.
Est-ce correcte ?
Merci.
tu peux essayer en coord. cylindriques et ces relations pourront te servir au 1.7)
sauf que ce n'est pas Rx et Ry mais Ru et Rv , u et v étant les vecteurs tournant dans xoy
mais tant que tu ne connais pas O=O(t) tu ne peux pas avancer.
il faut remarquer que R est normale à la trajectoire, donc il faut projeter la relation fondamentale sur la tangente à la courbe pour éliminer la réaction (inconnue)
et le plus simple est de prendre le repère de Frénet (si tu connais 
Je ne vois pas comment projeter le poids je n'ai pas l'angle entre la tangente à la courbe et le poid.
un vecteur directeur de la tangente en M à la courbe est: T =  (M) / ||
(M) / || || (en supposant
|| (en supposant  (M) non nul)
(M) non nul)
dans la base (er, e ,
, ) liée aux coord. cyl.
) liée aux coord. cyl.
 = RO' e
= RO' e + hO'
+ hO' 
et tu vas trouver un vecteur T constant dans cette base
pour calculer les projections de  et des forces sur la tangente, tu calcules simplement:
et des forces sur la tangente, tu calcules simplement:
 .T (produit scalaire)
.T (produit scalaire)
P . T
(R.T = 0 car R est normale à la trajectoire)
tu trouves finalement que O" = cste et tu intègres
sauf erreur
Ok je crois comprendre ce que tu voulais que je fasse.
En cylindrique :
|0
P = |0
|-mg
|R/ (R² + h²)
(R² + h²)
T = |0
|h/ (R² + h²)
(R² + h²)
|-R θ'²
 = |R θ"
= |R θ"
|h θ"
 .T = -R²θ'² /
.T = -R²θ'² / (R² + h²) + h²θ" /
(R² + h²) + h²θ" / (R² + h²)
(R² + h²)
R.T = 0
P.T = -mgh/ (R² + h²)
(R² + h²)
En appliquant le PFD :
-mgh/ (R² + h²) = m [-R²θ'² /
(R² + h²) = m [-R²θ'² / (R² + h²) + h²θ" /
(R² + h²) + h²θ" / (R² + h²)]
(R² + h²)]
Moi je tombe sur une équation différentiel...
Par contre en utilisant que les coordonnées cartésienne je trouve :
θ" = gh / (R² (R² + h²) + h)
(R² + h²) + h)
Erreur de calculs...
Mais je retrouve la même chose en coordonnées cartésienne.
On a donc :
θ(t) = -1/2 gh/(R²+h²) t² + K(t)
Mais on nous a demandé en fonction de z0 et v0.
Moi je pense que l'équation du mouvement ci-dessous est correcte :
z(t) = 1/2 (Rz/m - g) t² + vOzt + zO
Parce que le vecteur R et l'axe (Oz) forment un angle constant tout au long de l'expérience donc Rz est une constante et donc :
z(t) = hθ => θ(t) = 1/2 (Rz/mh - g/h) t² + (vOz/h)t + zO/h
...
1.7) Les composantes de la force de liaison :
Pour Rz :
On revient au PFD :
maz = -mg + Rz => Rz = m(az + g) = m(hθ" + g) = mg(1 - h²/(R²+h²))
D'ailleurs je retrouve la même chose en résolvant :
θ(t) = 1/2 (Rz/mh - g/h) t² + (vOz/h)t + zO/h = -1/2 gh/(R²+h²) t² + K(t).
Le K(t) doit surement être égal à : (vOz/h)t + zO/h
Pour Ry :
J'utilise les coordonnées cylindrique parce qu'avec ay = R(θ"cosθ - θ'²sinθ) il y a du θ' et du θ qui se baladent...
Pour les valeurs de θ' et θ, je pense que ce soit :
θ'(t) = (Rz/mh - g/h) t + (vOz/h) = + vOz/h
θ(t) = + vOzt/h + zO/h
...
Ry = may = mRθ" = -mgRh / R²+h²
Mais là Ry ne dépend pas du temps parce que j'ai écris la composante dans la base cylindrique. Dans la base cartésienne je pense pas que ça ne va pas le faire avec les sinus et cosinus, un gros tas quoi...
Pour Rx :
Même problème que sur Ry.
Merci encore pour ton aide !
O" = -C avec C = gh/(R2+h2)
O' = -Ct + O'o
O(t) = -C/2 t2 + O'ot + Oo
à t=0: v=vo = O'o (R2+h2)
(R2+h2)
et z=zo = h Oo
donc on trouve finalement O(t) en fct de vo et zo
pour le calcul de R il vaut mieux projeter dans le repère tournant: (er, e ,
, )
)
P + R = m  (M)
(M)
R = m  (M) + mg
(M) + mg 
R = -mRO'2 er + mRO" e  +(mhO" + g)
+(mhO" + g) 
je te laisse remplacer O" et O' par leur valeur



