Inscription / Connexion Nouveau Sujet
Mécanique du point
Bonsoir,
Voilà un exercice de mécanique sur les Energies et Travaux je ne comprends strictement rien...
Nous n'avons pas eu le temps de faire des exercices sur ce chapitre donc je patoge beaucoup...
Exercice
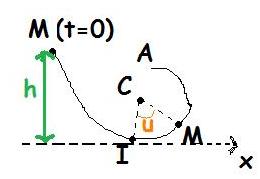
un mobile assimilé à un point matériel M de masse m se déplace sur un rail situé dans un plan vertical. Le rail comporte une partie IA constituée d'un demi-cercle de centre C et de rayon l.
On néglige tout fonctionnement et la liaison entre le mobile et le rail est unilatéral, c'est à dire que la reaction exercée par le rail sur le mobile ne peut changer de sens.
La position du point M lorsqu'il est à l'intérieur du demi-cercle est repérée par l'angle u=
A l'instant t=0, le mobile est lâché sans vitesse initiale à la hauteur h au dessus du I.
1a. Justifier qu'au cours du mouvement du mobile, l'énergie mécanique se conserve.
1b En déduire l'expression de la norme de la vitesse en M en fonction de h,l,u et g l'accélération de la pesanteur.
Si vous pouviez mettre votre développement pour ces 2 questions sa serait génial...
Merci, et Bonne année!
Antoine.
Tiens, clique, ça va te rappeler des souvenirs:
![]() Travail énergie (looping)
Travail énergie (looping)
Les seules forces entrant en jeu sont :
1. le poids de du mobile qui est une force conservative
2. la réaction du rail qui est normale à la trajectoire (travail nul)
D'où la conservation de l'énergie mécanique.
pour la 1b je devrais trouver v= en utilisant le théoréme de l'Energie Cinétique mais je n'arrive pas à prendre en compte le rayon l et l'angle u
j'ai une autre question qui me pose soucis.
En utilisant le principe fondamental de la dynamique et le résultat de la question précédente () exprimer à l'intérieur du demi-cercle, la norme R de la reaction
en fonction de h,l, u et g l'accélération de pesanteur.
Pour ma part j'ai travailler en coordonnée polaire avec origine C.
j'ai le poids
mais la réaction je ne trouve pas...
après je devrais faire une projection sur et
et
enfin isoler
Pouvez vous m'aider à trouver la réaction ?
Voici le schéma avec les coordonnées polaires:
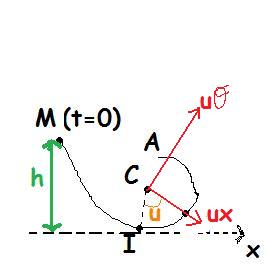
Il va en effet te falloir projeter sur les forces s'exerçant sur le mobile.
Cela te permettra de déterminer l'expression de l'accélération normale en appliquant le principe fondamental de la dynamique.
Détermine ensuite une seconde expression pour l'accélération normale en utilisant une formule reposant sur le rayon de la trajectoire et la vitesse du mobile.
En combinant les deux expressions de l'accélération normale, tu seras en mesure de déterminer la valeur de .
je ne trouve pas la relation entre les 2 accélérations m.=
+
et a= v²/R si ce sont ces 2 celles-ci qui faut utiliser..
Hé bien projette tout sur \vec{u_r} car si on décompose \vec{a} de la façon suivante:
On a:
tandis que ta première équation te donne:
En comparant les deux expressions de tu peux déduire la valeur de la réaction.


