Niveau licence

mécanique des sols stabilités des pentes

Posté par
Pierre_07 04-05-15 à 19:32

Bonjour,

J'ai quelques problèmes sur les méthodes de calculs à la rupture en stabilité des pentes voici mon probleme:

Je souhaite calculer un coefficient de sécurité F= $\frac{\tau_{max}}{\tau}$ , le critère de Coulomb s'écrit quant à lui $\tau= c'+\sigma'tan(\varphi')$ où $c', \sigma',\varphi'$ sont respectivement la cohésion effective, la contrainte normale effective et l'angle de frottement. De plus $\sigma=\sigma'+u$

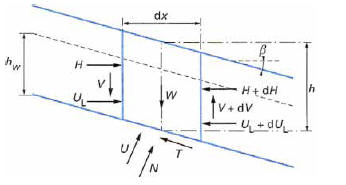
De plus l'hypothèse de pente infinie nous permet d'écrire que $V=0$ et que $H$ et $U_L$ s'équilibrent.
$T=\tau$
Donc je fais un bilan des efforts restant:

$U=Usin(\beta)\overrightarrow{x}+Ucos(\beta)\overrightarrow{y}$
$V=Vsin(\beta)\overrightarrow{x}+Vcos(\beta)\overrightarrow{y}$
$T=-Tcos(\beta)\overrightarrow{x}+Tsin(\beta)\overrightarrow{y}$
$W=-\gamma h dx \overrightarrow{y}$

Ensuite je choisis M un point tel que
$\overrightarrow{OM}= (0; -y; 0)$
Alors j'écris le PFS en moment et je trouve $y(U+V)sin(\beta)-yTcos(\beta)=0$ ce qui est proportionnel à la somme des efforts sur $\overrightarrow{x}$ donc j'ai deux équations et je n'arrive pas à conclure et surtout à trouver $T$ afin de pouvoir écrire mon coefficient de sécurité.

Je suis sensé trouver $\tau=\frac{c'+(\sigma-u)\tan(\varphi')}{F}$

je ne comprend pas comment utiliser le PFS sur ce problème, de plus j'ai un autre problème c'est qu'on écrit le poids comme $W=-\gamma hdx\overrightarrow{y}$ où $\gamma$ est le poids volumique ce qui est homogène à un poids sur une longueur... Enfin bref je bloque pas mal sur ce problème comme vous pouvez le constater.
Merci d'avance!

mécanique des sols stabilités des pentes