Inscription / Connexion Nouveau Sujet
Mecanique des solides indeformables
Bonjour la famille!
S'il vous plait j'ai rencontré un probleme sur cet exercice et j'aimerais bien avoir de l'aide
On considere le solide representé sur la figure
f(0) et f(x) ( en vecteur biensur) representent les forces par unité de longueur entre L/2 et L. On a f(x) =(ax+b)  . (f en vecteur).
. (f en vecteur).
1)determiner a et b en fonction de f0 et L
2) determiner le torseur par rapport a O, des forces appliquées solide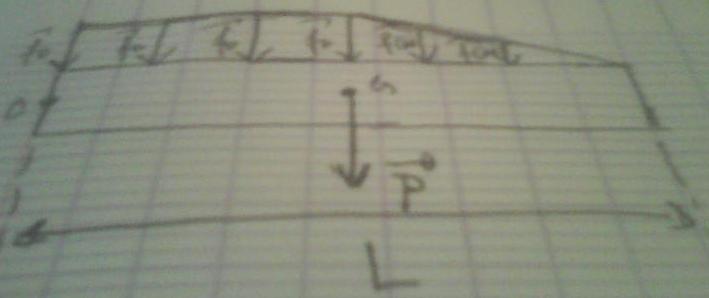
***Image recadrée***
Hello
f(L/2) = f0 = a x L/2 + b
f(L) = 0 = a x L + b
Tu as un système de 2 équations à 2 inconnues (a et b) à résoudre.
Quel est le moment du poids en O?
Pour les charges linéiques, calcule le moment élémentaire autour d'un point M situé à une distance x (tu distingues 2 cas 1) 0<x<L/2 puis 2) L/2<x<L )
Pour avoir a et b je fais:
Pour x [0, L/2] j'ai f(x) =f0 en vecteur
[0, L/2] j'ai f(x) =f0 en vecteur
Pour x=L f(x) =0
Tout calcul bien fait j'ai x=2f0/L et b=-2f0.
Or le torseur est un ensemble formé de F qui est sa resultante et M son moment. Or F=F0,L/2+P+FL/2,L.
F0,L/2=-f0L/2
P=-mg
FL/2,L= f(x) dx car f(x) varie sur cet intervalle.
f(x) dx car f(x) varie sur cet intervalle.
FL/2,L=-f0L/4
D'ou F=-(f0L/2 +mg)  .
.
Pour le moment je fais
M=MF[sub]0,L/2[/sub]+Mp+MF[sub]L/2,L[/sub]= OG^F0,L/2+OG^P+OB^FL/2,L. Avec B un point quelconque situé entre L/2 et L. OB=(L/2 + x)  . Mais j'ai l'impression que mes calculs sont bizarre
. Mais j'ai l'impression que mes calculs sont bizarre
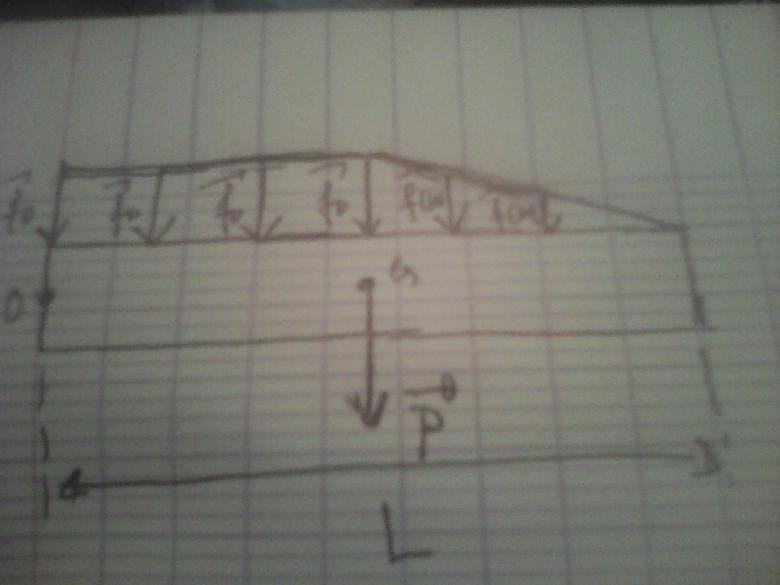
Tout va bien jusqu'au calcul des moments...
Premier point: peut on négliger ou pas la hauteur du solide?
On va dire oui dans un premier temps pour avancer sur le raisonnement, on ajustera ensuite:
En valeur algébrique
Pour un point situé à une distance x de O le moment élémentaire est:
Si 0<x<L/2
dM(x) = xf0dx
=> il faut alors intégrer entre 0 et L/2
Si L/2<x<L
dM(x) = xf(x)dx
= il faut intégrer entre L/2 et L
Pourquoi calculer le moment elementaire dM pour 0 x
x L/2?? Alors que sur cette intervalle f est constante? On applique le moment elementaire quant f varie( sauf erreur), comme sur [L/2, L] . Là, on aura un moment elementaire dM
L/2?? Alors que sur cette intervalle f est constante? On applique le moment elementaire quant f varie( sauf erreur), comme sur [L/2, L] . Là, on aura un moment elementaire dM
Pourquoi calculer le moment elementaire dM pour 0xL/2?? Alors que sur cette intervalle f est constante?
C'est toi qui vois ... Mais si le calcul de l'intégrale (au moins une fois dans ta vie) te permet de comprendre que tu te trompes lorsque tu appliques la résultante en L/2, il n'aura pas été inutile



